Strong Anticipation in Social Systems and
the Emergence of a Knowledge-Based Society
Loet Leydesdorff
University of Amsterdam, Amsterdam School of Communications Research (ASCoR)
Kloveniersburgwal 48, 1012 CX Amsterdam, The Netherlands
loet@leydesdorff.net . http://www.leydesdorff.net
Abstract
Reflexive agents not only communicate in terms of information exchanges, but also provide these exchanges with meaning from a hindsight perspective. This is an anticipatory mechanism because an expectation can then be specified. At the level of the social system, meaning can additionally be communicated. When meanings are variously codified (because of functional differentiation in the communication), the potential asynchronicity (∆t) in the updates provides the communication system with a second anticipatory mechanism. Interactions between these two anticipatory degrees of freedom can lead recursively to co-evolution and stabilization of expectations. However, the horizon of knowledgeable expectations can be expected to meta-stabilize the previously stabilized organization of expectations. A next-order selection may lead to globalization. Globalization can be modeled using the hyper-incursive formulation of the logistic equation, whereas stabilization is based on an interaction among two incursive subdynamics. A globalized system can be considered as a strongly anticipatory system which constructs its own future states. A strongly anticipatory system is no longer necessarily based on historical manifestations, but its operation can increasingly be knowledge-based.
Keywords: anticipation, social system, communication, globalization, hyper-incursion
1. Introduction
Dubois (2000) distinguished between weakly and strongly anticipatory systems. Unlike weakly anticipatory systems (Rosen, 1985), strongly anticipatory ones cannot provide predictions because they use anticipation for the construction of their future states. A social system reconstructs its future by providing new meaning to its past and can thus be considered as a strongly anticipatory system. In the modern era, for example, the social system continuously reconstructs itself at the interfaces between the techno-sciences and the economy in terms of techno-economic coevolutions.
Leydesdorff & Dubois (2004) have shown that one can use the incursive formulation of the logistic equation to model the social system. In this paper, I provide the hyper-incursive formulation of this same equation with an appreciation from the perspective of social systems theory (Luhmann, 1984; Leydesdorff, 2001). It has been suggested that the incursive and hyper-incursive equations can be used for the modeling of weakly and strongly anticipatory systems, respectively (Dubois and Resconi, 1992; Dubois, 2000). I submit that in the case of a social system, one is able to distinguish between the stabilization of expectations (in a knowledge infrastructure) and the globalization (knowledge base) that operates in terms of the construction of the next stage of the system by the system itself. Whereas stabilizations can be the consequence of an interaction and potential co-evolution between two (analytically independent) incursive subdynamics, globalization can be modeled using the hyper-incursive formulation of the logistic equation.
A stabilizing subdynamic can be expected to remain referential to the historical manifestations, while the globalizing one needs a third mechanism (e.g., decision-making) for the phenotypical manifestation of the hyper-incursive routine. Sequences of decisions can be ‘locked-in’ under the condition of network externalities (Arthur, 1988, 1989, 1994). After a lock-in a system can be expected to develop along a trajectory using a specific organizational form. Thus, the previous (e.g., natural) configurations can be rewritten by the knowledge-based system. The extent to which this subdynamic of self-organization prevails, can be studied empirically. A system containing three subdynamics (two anticipatory mechanisms and one for the organization) is able to produce a negative (Shannon-type) entropy in the mutual information exchanged among them (McGill, 1954; Abramson, 1962). This reduction of uncertainty can be used as an indicator of the system’s knowledge base at each moment of time (Leydesdorff, 2003a; Leydesdorff et al., 2004). In this study, however, I focus on the mechanisms generating the knowledge-based dynamics over time.
2. Interaction among Weakly Anticipatory Systems
The incursive formulation of the logistic curve was used to model and simulate a social system of interacting agents as an anticipatory system (Leydesdorff, 2003b; Leydesdorff & Dubois, 2004). The equation is:
x(t+1) = a x(t) (1 – x(t+1)) [1]
or, after a reorganization of this formula (Dubois, 1998), equivalently:
x(t+1) = a x(t)/ [1 + a x(t)] [2]
Using this model, one can generate an observer within a system. Figure 1 provides an example using a cellular automaton. By changing the parameter a one can generate observers entertaining different perspectives, and therefore with different biases in the observation (‘blind spots’). In addition to aggregation of—or equivalently taking the average among—observations, we will also consider the interaction among observations below.
|
Figure 1: The top-level screen produces a representation of the bottom-level one by using an anticipatory algorithm |
The average among two observers with parameters a and b, respectively, can be formulated (on the basis of Equation 2) as follows:
x(t+1) = {a x(t) / [1 + a x(t)]} / 2 + {b x(t)/ [1 + b x(t)]} /2 [3]
= {[1 +bx(t)] a x(t)+ [1 + ax(t)] b x(t)}/2
= {ax(t) +2ab x(t)2 + bx(t)}/2
= ½(a + b) x(t) + ab x(t)2
= [a x(t) + 1] [b x(t) + ½)]
or symmetrically:
= [b x(t) + 1] [a x(t) + ½)]
Using simulations, it can be shown that this ambiguity leads to uncertainty in the delineations of the observed systems (Figure 2). Since the two observers use different angles (parameters) for the observation, an uncertainty is generated. Interaction among the observations, however, can lead to stabilization of the observations albeit in a more complex representation (Figure 3).
|
|
|
|
Figure 2: Two observers (top level screens) observing a single screen (lower left) and each others observations (lower right screen). |
Figure 3: Two observations with their interaction effect in the lower right screen. |
The generation of interaction among the two observations in the top-level screens (Figure 3) can be modeled as a result of multiplication:
x(t+1) = d *{a x(t)/[1+a x(t)]}*{b x(t)/ [1+b x(t)]} [4]
In this formula the coefficient d represents the strength of the interaction. Let us elaborate this formula as follows:
x(t+1) = d *{a x(t)/[1+a x(t)]}*{b x(t)/ [1+b x(t)]} [4]
= d *{a x(t) [1 + b x(t)]} * {b x(t) [1 + ax(t)]} /{ 1 + ax(t) + bx(t) + ab x(t)2 }
= d * { a x(t) + a b x(t)2} { b x(t) + a b x(t)2} / { 1 + (a + b)x(t) + ab x(t)2 }
= d * {p x(t) + q x(t)2 + r x(t)3 + s x(t)4} / { 1 + (a + b)x(t) + ab x(t)2 }
Given appropriate choices of the parameters, this division can resolve into a quadratic equation and therefore provide us with a minimum. The minimum at each moment of time can generate a valley over time. The valley represents the trajectory of the system along a stabilized path (Waddington, 1957). This stabilization is the result of the dynamic extension of the interaction among two systems into a coevolution of mutual shaping among the expectations. The results of the interaction provide us with a richer representation than each of the interacting observations. For example, the results of the simulation exhibiting a representation of the system in the lower-left quadrant are provided in the lower-right quadrant of Figure 3. This representation is richer than those entertained by the individual (top-level) observers.
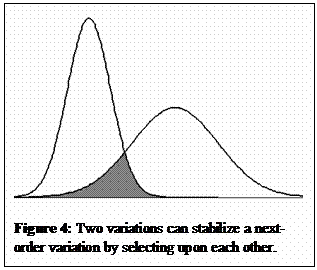In
other words: interaction allows the selections formalized in the right-hand
term of the logistic equation (that is, the feedback term [1 ‑ x(t)])
to operate upon each other in the multiplication. This leads to a quadratic
term (1 – 2x(t) + x(t)2) that is positive, but an order of magnitude
smaller than the original variation. Whereas each observation can be considered
as a selection from the phenotypical complexity, some selections can be
selected for stabilization (Figure 4). However, this assumes that the
system contains two independent anticipatory mechanisms that are able to
operate upon each other.
3. Global Hyper-Incursion versus Historical Stabilization
Under the condition of functional differentiation (Luhmann, 1984; Leydesdorff, 2001) the social system can be expected to contain two (analytically) orthogonal mechanisms for the anticipation, namely:
- the information exchanged can be provided with meaning from the perspective of hindsight;
- when the system is functionally differentiated, the codes of the communication are no longer synchronized ex ante. This asynchronicity provides the system with a second Δt.
While synchronizations take place at specific moments in time, the construction of meaning requires development along the time axis. This historical development stands orthogonally to the transversal updates among the functionally differentiated systems. The interaction between these two analytically different mechanisms of anticipation can be expected to organize stability in the historical manifestations of the strongly anticipatory system. The latter can be expected to develop in terms of fluxes. Stabilization can also be considered as a resonance among two selecting subdynamics.
Whereas some selections can be selected for stabilization, stabilizations can also be selected for globalization. However, this next-order selection presumes yet another axis within the system which has to be analytically different from the one of historical stabilization. The axis of globalization remains an expectation of a next-order or later subdynamic of the system. It emerges from the codification of meaning within the system and can then provide the historically organized system with a knowledge base for operating. However, this knowledge-based subdynamic operates differently from one which is rooted in a historically given system. Although the system remains phenotypically composed of different subdynamics, the next-order subdynamic one cannot appear without mediation. In other words, it remains a hypothesis.
The hyper-incursive formulation of the logistic equation enables us to formalize this hypothesis about the global dimension as follows (Dubois, 2000, 2003): [1]
x(t) = ax(t+1) [ 1 – a x(t+1)] [5]
or equivalently:
x(t) = a x(t+1) – a x(t+1)
xt = axt+1 – axt+12
axt+12 – axt+1 + xt = 0
xt+12 – xt+1 + (xt/a) = 0 [6]
For a = 4, xt+1 can mathematically be defined as a function of xt as follows:
xt+1 = ½ ± ½ √ (1 – xt) [7]
Note that this formula is no longer firmly based in the historical axis of forward-moving time. This system is unpredictable in the sense that it is not possible to compute its future states by knowing the historical conditions. As the system can only take one value at each time step, another mechanism must be made available to resolve this problem. Dubois (2003: 114f) proposed, for example, to add the following decision function u(t) for making a choice at each time step:
u(t) = 2 d(t) – 1 [8]
where u = +1 for the decision d = 1 (true) and u = –1 for the decision d = 0 (false).
Dubois (2003) emphatically noted that the decisions d(t) do not influence the dynamics of x(t), but only guide the system which itself creates the potential futures. In the social system, this guidance is provided by the historical organization of the system. Decision-rules can stabilize the organization over time. Both the stabilizing organization (for example, in institutions) and the globalizing self-organization of the fluxes of communications in different directions belong to the social system as subdynamics. The self-organization of the fluxes in the globalizing system of communications is constrained and guided by the historical organization of the stabilizing subdynamic. The two subdynamics can be expected to operate upon each other as different selection mechanisms (Leydesdorff, 2001).
4. Conclusion
Historical organization can be considered as one among a variety of subdynamics of the self-organization of communication in a knowledge-based system. Organization provides the historical retention mechanism for solving puzzles among the fluxes at the interfaces among functionally differentiated subsystems. The code of this organizational subsystem in society was identified by Luhmann (1975, 2000) as decision-making. Recursive decision-making by communications among reflexive agents enables the system to stabilize an expectation along a trajectory in terms of boundaries within an otherwise unorganized or differently organized environment.
The globalizing subdynamics counteracts this historical stabilization by potentially reducing the uncertainty against the arrow of time, that is, from the perspective of the expectations about the future as they are communicated, for example, in scientific discourses. The discourses entertain models of the systems under study. When these models are provided with meaning in other social systems (e.g., the economy), a knowledge base can be generated because decisions can be made increasingly informed at these interfaces. The hyper-incursive anticipation remains analytically independent of the historical realizations, but as a theoretically informed hypothesis it can be expected to interfere with the system’s history by reinforcing the relative weight of the system’s knowledge base in decision-making over time.
References
Abramson, N. (1963). Information Theory and Coding. New York, etc.: McGraw-Hill.
Arthur, W. B. (1988). Competing Technologies. In: G. Dosi, C. Freeman, R. Nelson, G. Silverberg, and L. Soete (Ed.), Technical Change and Economic Theory (pp. 590-607.). London: Pinter.
Arthur, W. B. (1989). Competing Technologies, Increasing Returns, and Lock-in by Historical Events. Economic Journal, 99, 116-131.
Arthur, W. B. (1994). Increasing Returns and Path Dependence in the Economy. Ann Arbor: University of Michigan Press.
Dubois, D. M. (1998). Computing Anticipatory Systems with Incursion and Hyperincursion. In D. M. Dubois (Ed.), Computing Anticipatory Systems: CASYS’97, AIP Proceedings Volume 437, pp. 3-29. American Institute of Physics, New York: Woodbury.
Dubois, D. M. (2000). Review of Incursive, Hyperincursive and Anticipatory Systems -- Foundation of Anticipation in Electromagnetism. In: D. M. Dubois (Ed.), Computing Anticipatory Systems CASYS’99 (Vol. 517, pp. 3-30). Woodbury, NY: Amercian Institute of Physics.
Dubois, D. M. (2003). Mathematical Foundation of Discrete and Functional Systems with Strong and Weak Anticipation. In: M. V. Butz, O. Sigaud, and P. Gérard (Eds.), Anticipatory Behavior in Adaptive Learning Systems. Lecture Notes in Computer Science 2684. Heidelberg: Springer.
Dubois, D. M., and G. Resconi (1992). Hyperincursivity: A New Mathematical Inquiry. Liège: Presses Universitaires de Liège.
Leydesdorff, L. (2001). A Sociological Theory of Communication: The Self- Organization of the Knowledge-Based Society. Parkland, FL: Universal Publishers.
Leydesdorff, L. (2003a). The Mutual Information of University-Industry-Government Relations: An Indicator of the Triple Helix Dynamics. Scientometrics, 58 (2), 445-467.
Leydesdorff, L. (2003b). Anticipatory Systems and the Processing of Meaning: A Simulation using Luhmann's Theory of Social Systems. Paper presented at the European Social Simulation Association (SimSoc VI workshop), Groningen.
Leydesdorff, L. (2004). Meaning, Anticipation, and Codification in Functionally Differentiated Systems of Communication. In: T. Kron, U. Schimank & L. Winter (Eds.), Luhmann Simulated – Computer Simulations to the Theory of Social Systems. Münster, etc.: Lit Verlag, forthcoming.
Leydesdorff, L., and D. M. Dubois (2004). Anticipation in Social Systems: The Incursion and Communication of Meaning. Int. J. of Computing Anticipatory Systems (forthcoming).
Leydesdorff, L., W. Dolfsma, & G. v. d. Panne. (2004). Measuring the ‘Knowledge Base’ of an Economy in Terms of Relations among ‘Technology, Organization, and Territory.’ Paper presented at the Annual Meeting of the Joseph Schumpeter Society, Milan, 10-12 June.
Luhmann, N. (1975): Interaktion, Organisation, Gesellschaft: Anwendungen der Systemtheorie. In: M. Gerhardt (Ed.), Die Zukunft der Philosophie (pp. 85-107). München. [In: Soziologische Aufklärung 3. Opladen: Westdeutscher Verlag, 1975, pp. 9-20.]
Luhmann, N. (1984). Soziale Systeme. Grundriß einer allgemeinen Theorie. Frankfurt a. M.: Suhrkamp [translated as Social Systems. Stanford: Stanford University Press, 1995].
Luhmann, N. (2000). Organisation und Entscheidung. Opladen: Westdeutscher Verlag.
McGill, W. J. (1954). Multivariate Information Transmission. Psychometrika, 19(2), 97-116.
Rosen, R. (1985). Anticipatory Systems: Philosophical, Mathematical and Methodological Foundations. New York: Pergamon Press.
Waddington, C. H. (1957). The Strategy of Genes. London: Allen & Unwin.
[1] There are two additional formulas which merit investigation:
xt = axt (1 – xt+1) [5a]
xt = axt+1 (1 – xt) [5b]
· Equation 5a evolves into x = (a – 1)/a = Constant. I submit that this evolution towards a constant through anticipation can be considered in modeling the self-reference of an (individual) identity.
· Equation 5b evolves into xt+1 = (1/a) {xt / (1 – xt)} Since the latter term approaches –1 as its limit value and the former term is a constant (1/a), this representation can alternate between itself and its mirror image. This subdynamic thus formalizes the reflexive operation.
Both these subdynamics can be expected to play a role in social systems.