Epilogue
(Evolutionary Economics and Chaos Theory: New Directions in Technology Studies, Loet Leydesdorff & Peter van den Besselaar (eds.). London: Pinter, 1994: pp. 180-192)
What I love best about the calculus is that (...)
it frees us from working with our imagination.
Leibniz (1692)
New Models of Technological Change: New Theories for Technology Studies?
Loet Leydesdorff
Can the interaction between evolutionary economics and non-linear systems theory help us to specify new perspectives for technology studies? How are contributions from economics, sociology, evolution and systems theory relevant to an understanding of the dynamics of technology in society? This question seems urgent at the end of this compilation of contributions from various disciplines. Is the whole more than the sum of its parts?
I shall argue that the theory of complex dynamic systems can guide us in clarifying these issues. The formal theory enables us to proceed from theoretical specification to generalization. Conclusions concerning the further development of technology studies can be drawn on the basis of the emerging paradigm, and normative implications for technology policies can be specified. However, this inference requires a series of reflexive steps.
First, it is necessary to deconstruct the biological metaphor in evolution theory. In cultural evolution theory, variation can no longer be considered as a consequence of “natural” or external selection. Nowadays, both the natural environment and the markets are increasingly changing due to technological developments. However, the assumption of a feedback--or a co-evolution--between the selecting macro-system and the micro-variation potentially closes the evolutionary system into a self-referential loop (Maturana 1978). “Variation” and “selection” should then be considered as sub-dynamics of the complex system. On the one hand, this change in perspective allows us to envisage that the category which was, for example, specified as the selecting instance at one moment, may have to be respecified as generating variation at a next moment. On the other hand, the respecification of evolutionary categories “on the fly” has implications for the epistemological status of theoretical specifications. The categorical meaning of the variables is then allowed to change, in addition to possible changes in the values of these variables.
While the discursive interpretation tends to become confused when both the theoretical categories and the values attributed to them change, the algorithmic simulation enables us to identify the various dynamics. By understanding variables as fluxes, one is able to distinguish change in the value of the variables from interactive effects affecting the variables themselves. The specification of theoretical categories, however, requires reflection based on the adoption of a specific--i.e. selective--perspective (cf. Hinton et al. 1986). In other words, the “phenotypical” behaviour of the model system is more complex than its composing (“genotypical”) dynamics, while only the latter can be made the subject of substantive theorizing (cf. Langton 1989).
The theoretical systems constitute another layer of complex (reflexive) systems on top of the complex social system(s) under study. The various paradigms compete in the effort to understand technological developments by reflexively organizing the complex systems under study. The lack of external standards would make it appealing to compare the explanatory power of the various discourses within another self-referential meta-discourse. But is a meta-discourse available that can contain sufficient complexity for the comparison?
The message of the post-modern philosophy of science has been precisely that such a comparison among “incommensurable” paradigms is no longer possible (cf. Kuhn 1962). The transition from variables in a spatial model to fluxes in an algebraic model, however, provides us with an additional degree of freedom in the discourse, since variables can be considered as instantiations of fluxes. The resulting discourse pays a price for being formal; it only refers to substantive specification (cf. Andersen 1992). Non-linear dynamics, therefore, can be considered as another partial perspective, but one that enables us to formulate an expectation about relations among discourses. In the final sections of this chapter, the application of this analysis to technology studies will lead to conclusions both with respect to the subject matter and with respect to the interdisciplinary organization among the contributing disciplines.
The reconstruction of evolution theory
What are the differences between biological and socio-economic theories of evolution? First, there is a difference with respect to the evolving unit of analysis, and second, this difference has epistemological implications. Although philosophers of biology have increasingly been aware that selection is internal to the complex system (e.g., Eldredge 1985; Freese 1988; Lee, this volume), practicing biologists may refer to “nature” or “natural” selection without necessarily deconstructing these concepts as theoretical attributions. In evolutionary economics, however, “selection environments” have been defined more abstractly than observable markets (Nelson and Winter 1977). Therefore, economic selection environments are obviously theoretically constructed, as are the units of variation. Neither the entrepreneur nor the firm, let alone the modern corporation are “naturally given”; they are the results of a stage of cultural evolution that has been achieved through human history. The analytical categories can no longer be attributed to an unambiguous referent, and consequently, the units of analysis themselves are reflexively constructed on the basis of previous understanding, i.e. within discursive networks (cf. Hesse 1980).
Given that the analytical categories themselves are theoretically constructed, various theories may differ profoundly in terms of their basic assumptions about units of analysis or, in other words, about the systems that are considered central to economic analysis. For example, while some contributions to evolutionary economics have drawn on the theory of the firm, others have argued that technologies or industries are the evolving systems. If one analyst provisionally equates different technologies with different production units, other scholars can provide us with counter-examples for this identification. Thus, cultural evolution theory requires more reflexivity about the evolving unit than biological evolution theory originally contained (Andersen 1992). Both “selection” and “variation” are theoretical attributions: variations are contained in the hypothesized systems as uncertainty in the distributions, while selections provide the uncertainty with feedbacks (cf. Allen, this volume). Since the processes under study are multi-layered, various interacting dynamics (of variation and selection) can be assumed. More than one selection may operate on a variation, and the various selections may interact. In general, the specification of these relations generates a model.
A feedback can reduce the uncertainty to a skewed distribution, but this selection does not yet transform the uncertainty into a signal (Bruckner et al., this volume). Only if the selecting system is sufficiently stable over time will it additionally be able to distinguish what it recognizes as variation from what is merely noise. Thus, the selecting system additionally pre-selects the communication by setting boundary conditions to the relevant variation (cf. David and Foray, this volume). However, these two negative feedbacks--one from the selection and one from the pre-selection by the self-referential system--can sometimes be combined into a positive feedforward. When this happens, evolution may begin.
But this is no longer “natural” evolution; it is rather the specification of an evolutionary model of the system under study which may also happen to be additionally identifiable in terms of events that have actually occurred. Observable history is the special case which happens to occur among ranges of other possibilities that the model can explore (e.g., Brunner, this volume).
Algorithmic simulation and discursive model specification
As is well-known from harmony theory, under specific conditions a system of various dynamics (e.g., feedbacks) may begin to resonate. Resonances provide complex systems with strong filters of noise, and therefore they are expected to have survival value (Simon 1969; Smolensky 1986). In the case of a multi-layered system, some subsystems may additionally drift in terms of their relevant resonances, while certain niches may better be shielded against variations in other parts of the system (Nijkamp and Reggiani, this volume). Cycles with different and changing frequencies should be expected. While biological theory has operated with natural units of time like seasons, years, and generations, cultural evolution theory has to specify one or more frequencies (or a spectrum) for each relevant context (cf. Kampmann et al., this volume).
In principle, each additional context introduces an infinite number of possible interactions. Without substantive specification--i.e., assumptions--the problem is usually non-computable. As noted, theoretical reflection is based on choosing a perspective: each specification operates as a selection device among other selection devices. The various theoretical specifications condition one another in the model system. By running the model, one may discover that in some regions the systems under study are inherently unstable. Whether stable solutions can be found remains an empirical question. Note that observable stability is the special case where action and counter-action balance. At other times, so-called “strange” or oscillating attractors can be shown (Greiner and Kugler, this volume; cf. Semmler 1986; Boldrin 1988). Thus, running a model provides us with insights into the potential dynamics of the non-linear system. While one may be able to find a local optimum in a simple model by trial and error, one needs to program stochastic variation into the complex system in order to have the computer explore the model’s state space for local or global optima (e.g., Rumelhart et al. 1986; Baum 1988; Langton 1989; Allen, this volume). Additionally, one can run the simulation a thousand or more times, and then develop its statistics.
In summary, the relations between modelling and theorizing generate a tension that drives the scientific research process. First, without sufficient specification the number of possibilities becomes rapidly non-computable (cf. Penrose 1989). Second, the appreciation of the results of a simulation requires its reflexive interpretation in terms of a theory. But without a simulation model one is not able reflexively to control the position that is (implicitly) chosen when understanding the complex system under study. Theoretical specifications assume a point of entrance into the state space of the model that they help to specify, and the results of the simulation may allow for theoretical inferences. But the latter have to be tested for their significance, since myriads of other inferences always remain possible.
Substantive theorizing requires a selective perspective, and therefore the theoretical reflections contain less complexity than the model system under study. Discursive theories specify sub-cybernetics (cf. Blauwhof, this volume). Note that there is no alternative: substantive theorizing is necessary for the specification of sub-dynamics. Upon theoretical specification of the various sub-dynamics (e.g., the market or the dynamics of innovation), probability distributions (variation) and conditional statements (selection) span the complex model in a multi-dimensional space. The specified mechanisms--formalized as equations--condition one another as selective devices. The interaction, however, is by definition non-linear, and therefore the outcome is foreseeably counter-intuitive from each partial perspective. The model system shows us the “unintended consequences” that cannot be specified by theorizing (cf. Giddens 1984). Albeit always dynamic, the model system can be considered additionally as evolutionary if it is allowed to use variation in order to explore and eventually to change the multi-dimensional space that the theoretical specifications have spanned (e.g., Phang and Allen, this volume). This may further complicate the theories, but the constraints on the appreciative understanding remain the same.
Theory feeds into the system ex ante for reasons of specification, and ex post in order to interpret the results. The results of the simulations require theoretical interpretation in the various traditions in order to improve the specifications in a next round. The discursive interpretation can be functional for the more precise specification of sub-cybernetics, and therefore theorizing may locally improve a model. This intellectual process is by definition discursive. Each theory will claim comprehensiveness, while meta-theoretically one expects various reflexive discourses to emerge as competing paradigms. The interaction among the discourses contains more complexity than each of the contributing disciplines, and this is made explicit by running the model. The discourses inform one another by discussing the various simulation results. In response to these interactions the axes of the reflexive discussions may gradually change. New developments in theorizing are made possible by exploiting these gains in creative recombinations (Lee, this volume; cf. Luhmann 1990).
Towards a general theory of complex dynamic systems
Is this hope for combinatorial profits the epistemological end of the road for scientific theorizing? Indeed, it is for substantive theorizing; one has to wait and see what will emerge in terms of new conjectures. But the general theory of complex dynamic systems additionally suggests a procedural expectation for comparing the various combinatorial solutions in a model system. This expectation can be derived from the central hypothesis that all “entropical” systems self-organize their thermal “death” (cf. Georgescu-Roegen 1971).[1] The potential “energy” contained in the initial conditions dissipates through the system as rapidly as possible according to the substantive dynamics of the system. In the complex system this is a complex process, like the whirl when flushing a toilet (Dyke 1993). But the processes are constrained by the selective instances that organize the fluxes (cf. Swenson 1989).
Both substantive and reflexive systems perform “life”-cycles in a hyper-space that includes the time dimension. Formally, time is just another dimension of the complex system. Differentiation is then equivalent to decomposability along the time axis. Self-organizing systems will tend toward differentiation along dimensions which are functional for the survival of the system. Differentiated systems build on and replace the lower-order ones by encompassing them as nearly decomposable sub-cybernetics (cf. Simon 1969). Complex dynamic systems can be compared in terms of their evolutionary “advancement”: the more differentiated they are, the more complexity the system is able to hold. The axes stand perpendicular and the interactions tend to be depressed.
If the higher-order system goes into crisis, the sub-cybernetics becomes less controled, and thus more active (as a muscle becomes hypersensitive upon its denervation). Eventually, a self-organizing system gives way to another self-organization of the chaos. But the various model systems can be compared in terms of their efficiency in organizing the fluxes of probabilistic entropy that they generate by operating (Swenson 1989). Different solutions refer to different optima, and one can program the model so that it is able to search for and to compare among alternatives (cf. Rumelhart et al. 1986; Anderson et al. 1988).
The reflexive understanding of the results, however, implies a necessary reduction of the underlying complexity by choosing a perspective. The scientific discourses can be considered meta-theoretically as cycles in relation to the hyper-cycle which is run in the model system (cf. Leydesdorff 1993). But if they are so formalized, no substantive language is left to integrate the various perspectives. While the algebraic understanding in terms of formal models and fluxes initially constituted only another discourse, this formal discourse can be developed into a discourse of a different order than the substantive theories that feed into it. As a hyper-cyclic model it enables us to reconstruct the complex interactions under study, and to distinguish the relative positions (and weights) of substantive specificiations by comparing them in terms of the dynamic analogon of the part of the variance (i.e., the probabilistic entropy flux) that they are expected to explain (Fig. 1.)
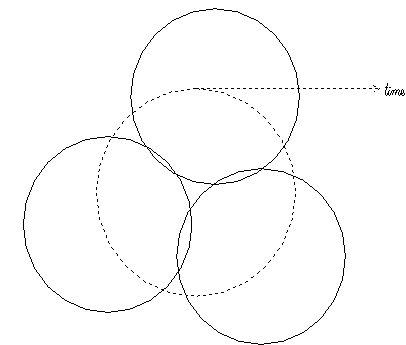 |
Figure 1. The hyper-cycle model
Technological developments as agents of change
Let us apply this model of competing but potentially interacting specifications to technology studies. As is well known, Schumpeter (1939) distinguished between innovations as changes in the shape of the production function reflecting the possibility to generate more output from less input, and changes along the production function as factor substitutions. Thus, two different dynamics were postulated: adjustment with reference to an equilibrium (or steady state), and the generation of innovation upsetting the movement towards equilibrium. Note that these two mechanisms stand orthogonally in terms of shifts along or perpendicular to the production function.
The regulatory (e.g., price) mechanism has captured the attention of (neo-)classical economics, but innovation has been considered as exogenous in this tradition. The identification of technological developments with the mechanism of change perpendicular to the production function provided evolutionary economics with a perspective for reducing the complexity in studying the dynamics of the system. Indeed, this perspective raises evolutionary questions, since the postulation of transitions among equilibrium states makes one wonder about trajectories or pathways in these transitions, their potential irreversibility, and the feedback between the emerging state and subsequent transitions.
Nelson & Winter (1977: 49) proposed that the feedbacks between technological trajectories and selection environments be ignored provisionally in favour of first developing conformable sub-theories about both mechanisms. The dynamics of innovation were then specified in terms of Markov chain models. In 1982, their comprehensive study provided theoretical specifications for technological developments both in relation and in opposition to neo-classical economics. Their stated aim was to endogenize the innovation mechanism into economic modelling, but the interaction terms were not yet specified.
Economic historians, however, have emphasized the interactive nature of the relations among technologies and markets (e.g., Rosenberg 1976). Sociologists have stressed the interdependence of variation and selection in social development processes (e.g., Bijker et al. 1987). Others have emphasized the path-dependent nature of technological developments and the consequent emergence of so-called “lock-ins” (Sahal 1981; David 1985; Arthur 1988). The idea that technological developments involve an “internal momentum” (e.g., Winner 1977) suggests, first, that developments relate to their own previous state(s). Each development has both a self-referential axis--since it extends from a previous stage--and an extent to which it interacts with relevant environments. If a “lock-in” among two axes occurs, a co-evolution (“mutual shaping”) can take off (cf. Nelson, this volume). The (super-)system internalizes the two contexts as degrees of freedom. This procedure can be recursively reiterated.
The interactive and recursive terms introduce higher-order dynamics into the models. For example, a trajectory of transitions between equilibrium states can be considered as the result of interactions between the dynamics of innovation and the market mechanism. The resulting pattern, however, can recursively enter into another relation to its selection environment, and then generate a technological regime. While the Markov chain models develop towards a single steady state along a “natural trajectory,” more than one trajectory can be developed if the transition matrix for the system is allowed to vary in relation to changing selection environments. For example, by using parallel and distributed computing Allen (1988) showed that in the curve of fish (“capital”) against fishing (“labour”) various densities--with their respective histories--could be originated in the simulation.
In the complex system, Nelson & Winter’s “search and selection processes” can with hindsight be considered as the organization at the interface between the two dynamics of technological innovation and market equilibria. Technological options (“search processes”) and market opportunities (“selection processes”) have to be combined socially into “heuristics” that are attributed to firms or aggregates of firms into industries. The functions of the social system have to be carried by local actors, but with reference to the complex system, these (aggregates of) actors should be considered as a distributed context that provides the evolving system with additional complexity, i.e. with social organization as a third degree of freedom. The dynamics along a third dimension can be used for selections upon first-order selections (on variations in a first dimension) using a second-order cybernetics. As noted, the operation of two selective mechanisms upon each other (“co-evolution”) allows for the possibility of a subsequent feedforward, including a provisional stabilization.
Dosi (1982: 154) once used the metaphor of a “cylinder” in a multi-dimensional space for describing a technological trajectory and its trade-offs. While a trajectory can still be considered as a dynamic trade-off between variation (“technological innovation”) and selection (e.g., “the market mechanism”), the direction or stabilization of a trajectory requires an additional context, e.g., a distribution of firms. Since firms are distributed, trajectories can only be localized provisionally and probabilistically. But if this (uncertain) localization offers specific advantages to enterpreneurs (cf. Atkinson & Stiglitz 1969; Sahal 1981), the local advantages can feedback to the dynamics of the system as a specific “selection environment”, and lead to “increasing dynamic returns” over time. Thus, the additional feedback can lock the trajectory into a regime (Allen, this volume).
In other words, the co-evolution of a specific combination of a selection environment with a probabilistically stabilized technological trajectory can lead to a globalized technological regime, or--in the case of an opposite sign--to the subsequent disintegration (“death”) of the configuration (cf. Abernathy and Clark 1985). While the trajectory tends to be locally stabilized, a regime tends to be globalized in a four-dimensional hyper-space. The regime is by definition in transition; the hyper-cycle of a regime remains “absent” if one studies observable events and relations in discursive models that use spatial metaphors (Giddens 1984).
Dosi’s (1982) metaphor of a “cylinder” appealed to a spatial representation, since the focus was on the “stabilized” trajectory. The four-dimensional technological regime (or “technological paradigm,” as Dosi prefers to call it) is uncertain with respect to the three-dimensional “cylinder” that it will consider as the representation of its past. In other words, the higher-order system contains a degree of freedom that enables it to make additional selections on lower-order stabilization. The globalized system is both more responsive and more resilient (since better buffered) than each of its composing dynamics.
For example, if we consider the car system as a typical regime in our time, this system is responsive to policy measures like taxing leaded petrol. However, such policy measures do not lead to a shift towards public transportation, since the system is able to cope with this disturbance in terms of innovation as one of its constitutive cybernetics. The normative implication is that, on the one hand, policies may be able deliberately to influence technological trajectories in terms of, among other things, the relative use of various production factors. On the other hand, similar policies can have a range of effects in the case of technological regimes because of the additional degree of freedom in the self-organizing system. Although the latter system is able to exhibit more responsiveness to policy measures (e.g., in terms of firm behaviour), one expects it to be resilient in restoring its own order.
In summary, the self-organizing regime is based on specific resonances among its constitutive cybernetics. Noise is continuously filtered out by the resonances among the lower-order systems. The self-organizing system returns to attracting states, and is therefore also self-cleaning as long as its hyper-cycle can be performed. The complex regime remains subject to the price mechanism, technological learning and social organization as its constitutive cybernetics; but it performs its own “life”-cycle, and thereby transforms the economy.
In an evolutionary model, one expects the various dynamics to be nearly decomposable: the subsystems interact in the observable events, but they tend to be reproduced as functional differentiations so that the system can organize as much complexity as possible. The emerging regime guides the order in the functioning of its subsystems by selecting ex post, while remaining a latent and ex ante condition for the instantiations at the next moment. As long as the lower-level systems run their cycles, the higher-order system is able to perform a hyper-cycle that sets the stage for dynamic developments at the lower levels. Since the sub-cybernetics tend towards functional differentiation (and therefore, near decomposability in the frequency domain), the various composing cybernetics have to be rearranged periodically with functional reference to the further development of the hyper-cycle. When the higher-order system tends towards crisis the lower-level systems become less controlled and therefore more active. Thus, the model can guide the search for clusters of innovations in the frequency domain (cf. Rosenberg and Frischtak 1984).
Surplus value at the theoretical level
Above, we have distinguished three functional dynamics for the emergence of a technological regime, namely the market system, technological innovation, and social organization in terms of firms and industries. The discourse of economics has introduced the market as an external referent, and therefore as a selecting device. As noted, substantive specification reduces complexity on the computational side (i) by setting a filter on the wealth of possible models, (ii) by raising the question of the economic interpretability of the results, and (iii) by focusing on economic data.
Recent attention to technological innovation in evolutionary economics has brought the dynamic aspect of innovative change into the picture. If understood as two dynamics of a super-system, the interaction terms are expected to generate “business cycles”, and thus to change the larger (social) system. This brings the sociology of technology into perspective. Thus, at least these three semantics are relevant, since they reflect interacting (but tendentially perpendicular) developments in the system.
Additionally, one would expect theories about all relevant interactions (cf. Simon 1973). But more importantly, one would expect a fourth orthogonal reflection of the system to be a subject of theorizing. This discourse addresses the problem of studying the hyper-cycle as an additional sub-dynamics. It abstracts from substances in the other dynamics, and reflects on fluxes instead of variables. Only reference to substance is left; the models tend to be formalized. The contribution, however, is to show that the actual regime or attractor is one among a range of attractors, and thus the model can sensitize the analyst to other possible dynamics.
One would expect the various discourses to interact, and to be functionally sorted again following interaction. The results may thus improve the understanding of technological developments in each of them, while not leading to a single comprehensive representation of the complexity of the processes under study. Each of the representations can specify sub-cybernetics in terms of expectations, but the specification of their interaction in the simulation model provides us with an additional angle to control for the quality of the expectation. Note that one can no longer predict, since the interactive effects are expected to be different from the expectation. But the interactive discourse is able to control for the quality of the expectation ex post, and it guides the specification of hypotheses on the basis of the results of simulations.
The new paradigm is based, among other things, upon the powerful tools of advanced computing for studying relations among specifications in non-linear models. The possible occurrence of irreversible thresholds in stochastic processes, the occurrence of bifurcations and strange attractors can be explored by using nested feedback loops for the recursive reduction of uncertainty. This discourse is mathematical; it uses a formalized language in which models can be formulated without a necessary relation to a specific instantiation in a system under study. Therefore, it allows one to generalize from the specifications to the state space, and in principle to suggest states other than those which are intuitively accessible. Thus, the system is able to bootstrap from specification to generalization. Note the analogy with the relation between stabilization and globalization.
The specification of the structural mechanisms that reduce the complexity can only be achieved by empirical research at the sub-systems level. Grandiose and comprehensive schemes do not help us further, since each context in itself adds an infinite range of possibilities for the further development of the model. Integration can only mean elaboration of the theoretically useful differentiations in a reflexive discourse. For example, on the basis of previous knowledge about the aircraft industry a researcher might have reason to expect certain innovation patterns in the helicopter industry (cf. Saviotti 1988). Only by carefully testing the expectations based on the former industry in the latter case can one stepwise improve the understanding, and consequently the models. The choice of case-studies, however, should anticipate the need for hypothetical generalization and formalization. Cases should be based, among other things, on considerations of sample choice in relation to populations. Remember that populations have first to be theoretically constructed, since one can no longer assume that they are given “naturally”. The discourses can inform one another with respect to theoretical expectations, but they develop self-referentially. Additionally, the various bodies of knowledge interact reflexively as “situated” perspectives by contributing to the further specification of models (cf. Haraway 1988).
Some normative implications
Considerations about the expected relations between technological trajectories and technological regimes provide us with a lead for the specification of normative implications. As noted, technological trajectories can be imagined in terms of three-dimensional pictures, while technological regimes organize themselves in the four dimensions of a hyper-space. Policies, however, cannot deliberately “steer” complex dynamic systems, but only generate feedback on their “instantiations.” The technological regime can be expected to react in an counter-intuitive way, and the intentional factors in the policy measures are self-referentially fed back into the political system as disappointments and occasions for learning (Luhmann 1990). Thus, the self-organization paradigm tends to emphasize the functions of subsystems; the degree of interaction remains an empirical question.
The more the developing regime is on the edge of crisis, the more receptive it will be to signals from its environments. Therefore, one might expect policies to be most effective when they support the “creative destruction” of hyper-cyclic regimes. Schumpeter’s well-known “creative destruction” disturbs the system, and thereby generates room for innovation along new trajectories. As noted, the more the system disintegrates, the more active the sub-cybernetics can be. However, one should be aware that the resulting processes are self-organizing, and reflexively responsive. Thus, new policies have to be invented from time to time.
In concreto, this conclusion means that policies should support emerging trajectories. While the regime (e.g., the car system) can be expected to restore its own order, taxing leaded petrol may be helpful for developing catalysts or cleaner engines. Among the various sub-cybernetics distinguished above, the one most accessible to the political process is the dynamics of social organization (Etzkowitz, this volume). As noted, intervention at the level of each sub-cybernetics can be functional, since the regime is always challenged by disturbances in its sub-cybernetics. From this perspective, the debate over socialist intervention and liberal laissez-faire has grown obsolete: today’s regimes contain both the dynamics of markets and those of social organization. Nowadays, the crucial question is whether interventions will prove to be functional in disturbing the ongoing process without laming it.
The political process has to organize the legitimation for intervention, but the intervention has to be assessed in terms of its effects in the relevant technological systems. Whenever two systems interact during the intervention, they can be expected to be functionally sorted thereafter. Note that this perspective provides us with a counter-intuitive set of evalutive standards for political action: not the effectiveness, but the (largely unintended) effects have to be assessed by a reflexive policy maker. The more reflexive policy maker will wish to register the unexpected effects, and to update his/her expectations. But since political expectations are normatively embedded, technological developments continuously generate tensions at the cultural level. These tensions can be considered as challenges to the future of technology studies.
References
Abernathy, W. and Clark K. (1985), ‘Innovation: mapping the winds of creative destruction’, Research Policy, vol. 14, pp. 3-22.
Allen, P. M. (1988), ‘Evolution, innovation and economics’, in Dosi et al. (1988), pp. 95-119.
Andersen, E. S. (1992), Artificial Economic Evolution and Schumpeter, Aalborg: Institute for Production, University of Aalborg.
Anderson, P. W., Arrow, K. J. and Pines, D. (eds.) (1988), The Economy as a Complex Evolving System, Reading: Addison-Wesley
Arthur, W. B. (1988), ‘Competing Technologies’, in Dosi et al. (1988), pp. 590-607.
Atkinson, A. and J. Stiglitz (1969), ‘A New View of Technological Change’, The Economic Journal, vol. 79, pp. 573-8.
Baum, E. B. (1988), ‘Neural Nets for Economists’, pp. 33-48 in Anderson et al. 1988.
Bijker, W., Hughes, T. P., and Pinch, T. (eds.) (1987), The Social Construction of Technological Systems, Cambridge, Mass.: MIT.
David, P. A. (1985), ‘Clio and the Economics of QWERTY’, American Economic Review, vol. 75 (2), pp. 332ff.
Dosi, G. (1982), ‘Technological paradigms and technological trajectories’, Research Policy, vol. 11, pp. 147-62.
Dosi, G., et al. (eds.) (1988), Technical Change and Economic Theory, London: Pinter.
Dyke, C. (1993), ‘Addition Accretion Accumulation Acceleration: Technology and Nonlinearity’, Manuscript for the Workshop New Developments in Technology Studies: Evolutionary Economics and Chaos Theory, Amsterdam, 1993.
Eldredge, N. (1985), Unfinished Synthesis: biological hierarchies and modern evolutionary thought, New York/Oxford: Oxford University Press.
Freese, L. (1988), ‘Evolution and Sociogenesis” Parts I & II, pp. 53-118 in E. J. Lawler and B. Markovsky (eds.), Advances in Group Processes, Vol. 5, Greenwich, CT: JAI Press.
Gabisch, G. and Lorenz, H-W. (1987), Business Cycle Theory, Berlin, etc.: Springer.
Georgescu-Roegen, N. (1971), The Entropy Law and the Economic Process, Cambridge, Mass.: Harvard University Press.
Giddens, A. (1984), The Constitution of Society, Cambridge: Polity Press.
Haraway, D. (1988), ‘Situated Knowledges: The Science Question in Feminism and the Privilege of Partial Perspective’, Feminist Studies, vol. 14, pp. 575-99.
Hesse, M. (1980), Reconstructions and Revolutions in the Philosophy of Science, London: Harvester Press.
Hinton, G., McClelland, J. L., and Rumelhart, D. E. (1986), ‘Distributed Representations’, in Rumelhart et al. (1986), Vol. I, pp. 77-109.
Kuhn, T. S. (1962), The Structure of Scientific Revolutions (Chicago: University of Chicago Press).
Langton, C. G. (1989), ‘Artificial Life’, in C. G. Langton (ed.), Artificial Life, Redwood City, etc.: Addison Wesley, pp. 1-47.
Leibniz, G. W., Letter to Christiaan Huygens, January 8, 1692, in C. Huygens, Oeuvres Complètes, The Hague: Nijhoff, Vol. X, at p. 227.
Leydesdorff, L. (1993), ‘”Structure”/”Action” Contingencies and the Model of Parallel Distributed Processing’, Journal for the Theory of Social Behaviour, vol. 23, pp. 47-77.
Luhmann, N. (1990), Die Wissenschaft der Gesellschaft, Frankfurt a.M.: Suhrkamp.
Maturana, H. R. (1978), ‘Biology of Language: The Epistemology of Reality’, in G. A. Miller and E. Lenneberg (eds.), Psychology and Biology of Language and Thought. Essays in Honor of Eric Lenneberg, New York, etc.: Academic Press, pp. 27-63.
Nelson, R. R., and Winter, S. G. (1977), ‘In search of useful theory of innovation’, Research Policy, vol. 6, 36-76.
Nelson, R. R., and Winter, S. G. (1982), An Evolutionary Theory of Economic Change, Cambridge, Mass.: Belknap.
Penrose, R. (1989), The Emperor’s New Mind, Oxford: Oxford University Press.
Rosenberg, N. (1976), ‘The direction of technological change: inducement mechanisms and focusing devices’, in Perspectives on Technology, Cambridge, etc.: Cambridge University Press, pp. 108-25.
Rosenberg, N., and Frischtak, C. R. (1984), ‘Technological Innovation and Long Waves’, Cambridge Journal of Economics, vol. 8, pp. 7-24.
Rumelhart, D. E., McClelland, J. L., and the PDP Research Group, (1986), Parallel Distributed Processing, Cambridge, MA/ London: MIT Press.
Sahal, D. (1981), Patterns of Technological Innovation, Reading, Mass.: Addison Wesley.
Saviotti, P. P. (1988), ‘Information, variety and entropy in technoeconomic development’, Research Policy, vol. 17, pp. 89-103.
Schumpeter, J. (1939), Business Cycles: A Theoretical, Historical and Statistical Analysis of Capitalist Process, New York: McGraw-Hill.
Semmler, W. (ed.) (1986), Competition, Instability, and Nonlinear Cycles, Berlin, etc.: Springer.
Simon, H. A. (1969), The Sciences of the Artificial, Cambridge, MA/ London: MIT Press.
Simon, H. A. (1973), ‘The Organization of Complex Systems’, in H. H. Pattee (ed.), Hierarchy Theory. The Challenge of Complex Systems, New York: George Braziller.
Smolensky, P. (1986), ‘Information Processing in Dynamical Systems: Foundations of Harmony Theory’, in Rumelhart et al. (1986), Vol. I, pp. 194-281.
Swenson, R. (1989), ‘Emergent Attractors and the Law of Maximum Entropy Production: Foundations to a Theory of General Evolution’, Systems Research, vol. 6, no. 3, pp. 187-97.
Winner, L. (1977), Autonomous Technology: Technics Out of Control as a Theme in Political Thought, Cambridge: MIT Press.