

(8) The Generation and Communication of Meaning in Social Systems
 Windows Program ( 1.5MB / .EXE ) | Loet Leydesdorff loet@leydesdorff.net University of Amsterdam ASCoR Amsterdam, North Holland Netherlands |
Description:
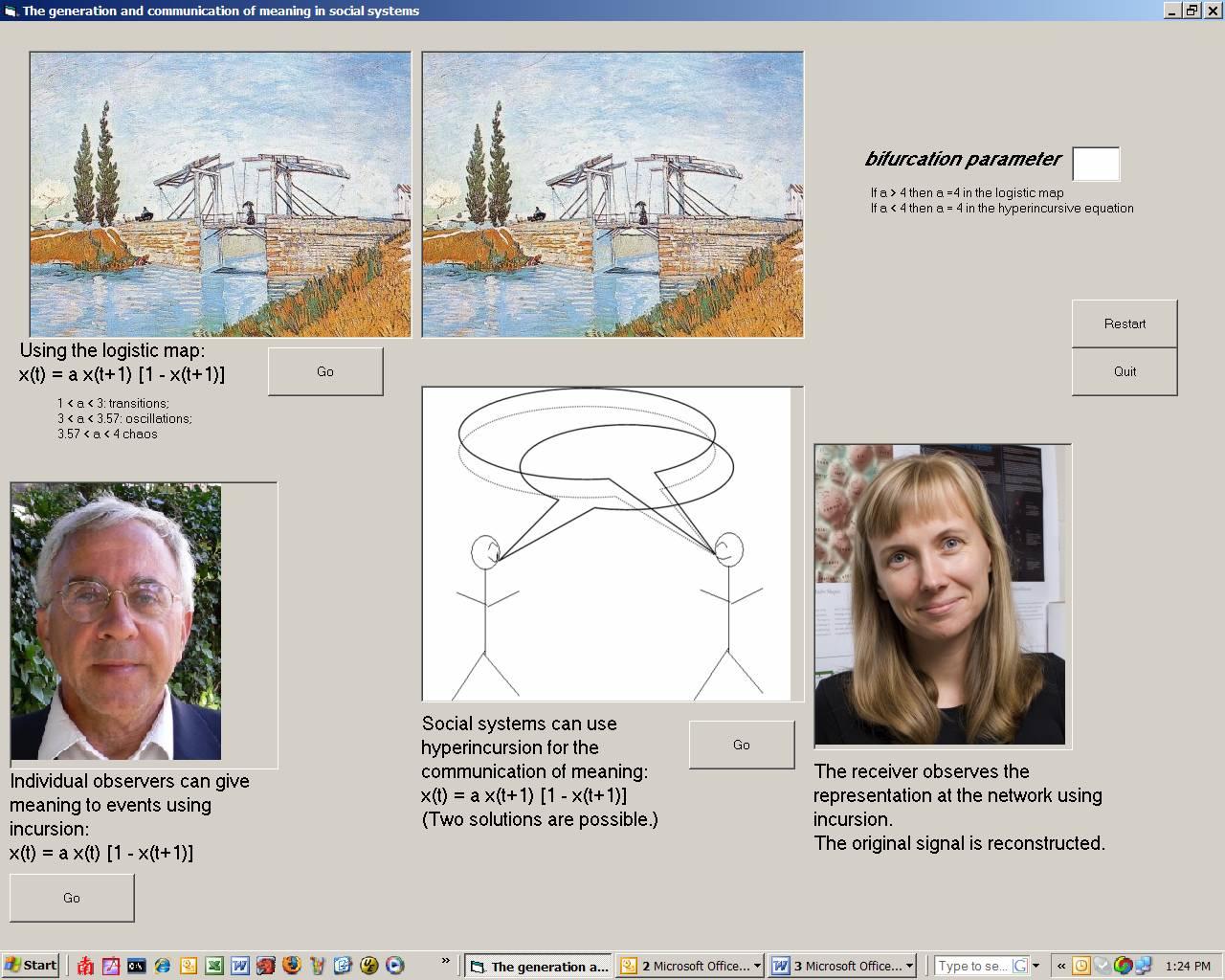
The program simulates the recursive, incursive, and hyper-incursive
development of a representation (in this case Van Gogh’s painting of
the bridge of Arles). It can be shown that the incursive formulation of
the logistic equation models not only the generation of an observer
(Leydesdorff, 2005), but also the operation of a social system
(Leydesdorff & Dubois, 2004). In addition to the communication of
information, social systems also communicate meaning. Meaning can be
generated incursively, but cannot be communicated without
hyperincursion.
Scientific Value: The sociological domain is different
from the psychological one insofar as meaning can be communicated at
the supra-individual level. The computation of anticipatory systems
enables us to distinguish between these domains in terms of weakly and
strongly anticipatory systems with a structural coupling between them.
Anticipatory systems have been defined as systems which entertain
models of themselves. The model provides meaning to the modeled system
from the perspective of hindsight, that is, by advancing along the time
axis towards possible future states. This can be modeled using
incursion: unlike a recursive routine, incursion operates both on the
previous and the current state of the system. Strongly anticipatory
systems use expectations for constructing their current states. The
dynamics of weak and strong anticipations can be simulated as incursion
and hyper-incursion, respectively. Hyper-incursion generates “horizons
of meaning” among which choices have to be made by incursive agency.
The simulations show this for x(t) = a x(t+1) (1 - x(t+1) → x(t+1) =
½ ± ½ √[1 – (4/a) x(t)] The choice between the
plus and the minus sign in this simulation is random.
Educational Value: The simulation makes the abstract
concepts of the (Rosen’s) mathematical theory and (Dubois’s)
computation of anticipatory systems accessible for a visual
appreciation. First, for values of the bifurcation parameter smaller
than four, oscillations and chaos can be generated using the logistic
map. Second, one can understand that providing meaning to the
representation means a specific selection (using the incursive
equation). The strength of this incursion becomes clear at the
receiving end when the picture is communicated by the social system
hyperincursively. The receiver is able to reconstruct the original
representation, but only in the case of one of the two possible
solutions of the quadratic equation.
References to Publications:
Related Projects:
http://www.ulg.ac.be/mathgen/CHAOS/CASYS.html