| 50% market shares of
Technologies A and B |
 |
|
|
time |
||
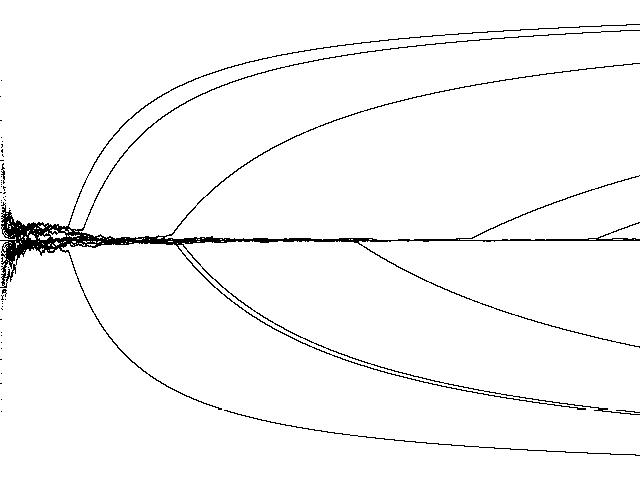
| Figure 1. Arthur's model as specified in Table 2; after ten simulation runs (10,000 adopters) |
The Triple Helix: An Evolutionary
Model of Innovations
Research Policy (forthcoming)
Science & Technology Dynamics, Nieuwe Achtergracht 166, 1018 WV Amsterdam, The Netherlands
loet@leydesdorff.net; http://www.chem.uva.nl/sts/loet/
Abstract
Arthur's (1988) model of the "lock-in" can be extended to the case of two and even three sources of random variation. Thus, one can model a triple helix of university-industry-government relations. In the case of two sources the stabilization of a technological trajectory is enhanced, while in the case of three a complex regime can be generated. Conditions for lock-in, lock-out, return to equilibrium, substitution, etc., are specified in relation to the assumed complexity of the dynamics under study and with reference to the stage of development, that is, before or after lock-in. Some normative implications of the triple helix model of innovations can be specified.
Introduction
The boundaries between public and private, science and technology, university and industry are in flux. Universities and firms are assuming tasks that were formerly the province of the other sectors. Shaping these relations is increasingly a subject of science and technology policies at different levels. University-industry-government relations can be considered as a triple helix of evolving networks of communication (Etzkowitz & Leydesdorff 1997). This "triple helix" is more complex than the mutual interactions between the "double helices" on which it rests.
Co-evolutions between technological developments and their cognitive and institutional environments change the knowledge infrastructure (Nelson 1994; cf. Freeman and Perez 1988). In a triple helix configuration, research, technology, and development networks increasingly change the relevant environments for R&D (Gibbons et al. 1994). New research agendas are constructed at cooperative research centers, on the Internet, or in virtual research institutes.
The triple helix thesis has meanwhile been elaborated into a recursive model of how an overlay of interactions operates on the institutional carriers. The institutions retain the hitherto best possible fits. Market selections, innovative dynamics, and network controls operate on these configurations using their respective codes of communication (e.g., prices; cf. Luhmann 1984 [1995]). Negotiations and translations at the interfaces induce adaptation mechanisms in the institutional arrangements (Leydesdorff 1997a).
Whereas two dynamics tend to coevolve into trajectories, a regime of transitions between trajectories is expected to emerge as one is able to recombine the historical contingencies in a network overlay. Using this overlay among the helices, the appreciation of hierarchical centers of control can be changed dynamically (Gibbons et al. 1994). Niche management and human capital management become crucial issues of policy formulation (Biggiero 1998; Leydesdorff and Etzkowitz 1998a).
For example, aircraft flight can be considered as a regime, while various trajectories can be recognized in the development of airplanes (Constant 1980; Mowery and Rosenberg 1981). The regime develops at the super-systemic level: one or more technological trajectories can combine dynamically with a market structure and institutional control at the national and/or the corporate level. The observable continuity in the development of a trajectory may be based on a coincidental "lock-in" that defines a standard for developing this technology (David 1985; Arthur 1988). The composing elements of a regime are expected to build upon their respective trajectories; the different subsystems select upon each other along these trajectories.
Selection is a recursive operation. If a single selection prevails, one can appreciate this as a result of the operation of the market. Innovation, however, tends to upset the movement of the market towards equilibrium (Nelson & Winter 1977). In the case of a mutual shaping between two dynamics (e.g., markets and technologies) a coevolution is expected as a result of selections by the systems upon each other: some selections are then selected for stabilization or, in other words, along a trajectory over time.
A regime can be considered as a meta-stabilization or, in other words, a selection on the stabilizations, that is, a globalization (Leydesdorff 1994). The third selector operates upon the coevolutions between the double helices. The triple helix is expected to exhibit a complex dynamics. A complex super-system, however, tends to develop "near decomposability" over time (Simon 1969). If integration were to fail, crisis would prevail. Thus, management and policy-making are locked-in as a reflexive helix to the co-evolutions between markets and technologies along trajectories.
How is the trade-off between differentiation and integration to be controlled? What is to be considered as optimal in different stages of the technology life-cycles? A complex dynamics allows for more than a single perspective. From each perspective one is able to develop a theoretical appreciation, but the perspective implies a specific reduction of the complexity (Luhmann 1984; Leydesdorff and Etzkowitz 1998b). For example, the technological trajectories generated in the interactions between markets and technologies have been, among other things, a theoretical focus of evolutionary economics (e.g., Rosenberg 1976; Nelson and Winter 1982). Analogously, the sustained interaction between state control and markets may lead to trajectories in the political economy. These need not be knowledge-intensive. Sustained interaction between state control and science-based innovations can lead to rigidities in, for example, the energy household (cf. McKelvey 1997).
When the three dynamics (that is, markets, innovation, and control) operate in a competitive mode (that is, as degrees of freedom in the model), the complexities and flexibilities of a triple helix network system are generated. Uncertainties in the relations between the helices open windows of potential innovation (and conflict) in (sub-)systems that otherwise have to be reproduced. Because the emerging order of the regime is pending and exerting selection pressure, the interactions between the subdynamics are entrained in evolutionary drifts (Kampmann et al. 1994). Arthur (1988) has shown that drifts trigger new lock-ins under specifiable conditions of increasing returns.
While Arthur (1988 and 1989) studied this process in the case of a single
source of variation —the random arrival of adopters on a market with competing
technologies— I shall extend his model systematically to two and then to
three sources of variation. My argument will be that (i) in the case of
a single source of variation, prolonged periods of equilibrium are possible
under specifiable conditions. Lock-in, however, is (ii) enhanced in the
case of two interacting dynamics. The interaction factors are crucial,
and (iii) only if these are reflexively declared will a triple helix exhibit
patterns of complex behaviour. Various policy implications follow from
this argument.
A further elaboration of Arthur's (1988) model
Arthur (1988 and 1989) specified why one should expect a lock-in in the case of competing technologies, randomness in initial purchasing behaviour, and absorbing barriers in the case of network externalities. A random walk will necessarily reach one of the barriers. From an evolutionary perspective, the absorbing barriers can be considered as structural selectors on the variation: the disturbance is locked in when the noise from the acting system reaches the level of a signal for the receiving system.
In other words, this model implies assumptions with respect to two systems of reference: the competition between technologies and the increasing returns on the market. While David (1985) and Arthur (1988) were mainly interested in the historical origins of lock-in in terms of consumer behaviour, I shall focus on what lock-in means for the receiving (market) system. This system of reference makes the discussion a bit more abstract, but it enables us to study systematically questions about preventing lock-ins and about how a lock-in can be disturbed to the extent of a potential "lock-out." From the perspective of the receiving system, it does not matter how the lock-in was generated. Thus, these (sub-)dynamics can be distinguished analytically.
Let me first shortly recapitulate Arthur's (1988) model: two competing
technologies are labeled A and B. These are cross-tabled
with two types of agents, R and S, with different "natural
inclinations" towards technologies A and B. In Table
1, aR represents the natural inclination of R-
agents towards type A technology, and bR an (in
this case, lower) inclination towards B. Analogously, one can attribute
parameters aS and bS to
S-agents
(bS > aS).
| Technology A | Technology B | |
| R-agent | aR + rnA | bR + rnB |
| S-agent | aS + snA | bS + snB |
Table 1. Returns to adopting
A
or B, given nA and nB previous adopters of A and
B.
(The model assumes that aR >
bR
and that bS > aS. Both r and s are
positive.)
The network effects of adoption (r and s) are modelled as independent terms, again differently for R-type agents and S- type agents. The appeal of a technology is increased by previous adopters with a term r (lower case) for each R-type agent, and s for S-type agents. If R-type and S-type agents arrive on the market randomly, the theory of random walks predicts that this competition will lock-in on either side (A or B).
The model is elegantly simple and it can easily be programmed (Leydesdorff and Van den Besselaar 1997). Table 2 provides the algorithm in BASIC. The parameter (aR, bR, aS, bS, r, and s) can be varied, and different scenarios can thus be tested.
| 10 INPUT N
20 SCREEN 11: WINDOW (-2, 0)-(N, 100): CLS 30 FOR J = 1 TO 25 40 LINE (-2, 50)-(N, 50) 50 RA = .8: RB = .2: SA = .2: SB = .8: NA = 1: NB = 1: s = .01: r = .01 60 RANDOMIZE TIMER 70 FOR I = 1 TO N 80 XX = RND 90 IF XX < .5 GOTO 100 ELSE GOTO 140 100 RETURNA = RA + r * NA: RETURNB = RB + r * NB 110 IF RETURNA > RETURNB THEN NA = NA + 1 ELSE NB = NB + 1 130 GOTO 160 140 RETURNA = SA + s * NA: RETURNB = SB + s * NB 150 IF RETURNA > RETURNB THEN NA = NA + 1 ELSE NB = NB + 1 160 Y = NA + NB: Z = 100 * NA / Y 170 PSET (Y, Z) 180 NEXT I 190 NEXT J 200 END |
| Table 2 Code for the simulation of Arthur's (1988) model. Source: Leydesdorff & Van den Besselaar (1998). |
| 50% market shares of
Technologies A and B |
 |
|
|
time |
||
| Figure 1. Arthur's model as specified in Table 2; after ten simulation runs (10,000 adopters) |
Figure 1 shows the results of ten runs of simulation in a population of 10,000 adopters with the parameter values used as provided in Table 2 (that is, 0.8 for aR and bS, 0.2 for aS and bR, and 0.01 for r and s). The line in the middle of the figure corresponds to a 50% market share for each technology. As predicted, lock-ins occur in all cases, although not necessarily before the end of the simulation using 10,000 adopters.
Note that the network effects are generated endogenously as a consequence of the values of parameters r and s. If one reduces these two parameters by 50% to 0.005 in the above model, lock-in will often fail to occur in a population of this size (10,000 adopters). The absorbing barriers are not caused by external (e.g., market) conditions, but by structural effects in a random walk with path-dependent feedback.
Elsewhere, we have tested this model extensively for its sensitivity to changes in parameter values (Leydesdorff and Van den Besselaar 1998). The main findings were:
1. Lock-ins are robust against changes in parameter values by orders of magnitude. First, a technological breakthrough affecting the natural inclinations does not lead to a lock-out and consequent substitution of a lock-in of the other technology. Second, strong reduction of the network effect for the winning technology (e.g., r) or, alternatively, enhancement of the network effect of the losing technology (in this case, s) by orders of magnitude does not change the configuration.
2. If one forces a "lock out" by further increasing (or decreasing) parameter values by orders of magnitude, the replacement pattern reverts to the curve for lock-in of the other technology. Figure 2 illustrates this case. Although highly unlikely in the case of increasing returns, substitution will be fast and ordered if successful.

time
Figure 2
Forcing technological "lock-out" and possible
return to equilibrium (20,000 adopters)
These rapid, but ordered substitution processes have hitherto been insufficiently understood from the perspective of evolutionary modelling. In a classical study, Fisher & Prey (1971) analyzed 17 cases of technological substitution. The cases included both product and process innovations (e.g., synthetic versus natural fibres and different furnace technologies). The main finding was that the rate of a substitution in all the cases, once begun, did not change throughout its history. This rate is not a simple measure of the pace of technical advance, but is determined by the evolutionary mechanism underlying substitution.
The simulation results show that substitution processes are expected to follow the lock-in line of the substituting technology. Evolutionary networks can be considered as hyper-networks that are able to suppress relevant subdynamics (cf. Bruckner et al. 1996). It is not the emergence of a new technology, but the balance between the dynamics of the interlocking networks that determines the dissolution of one lock-in or another given a choice between competing technologies (cf. David & Foray 1994).
3. There is a window for return to equilibrium if the market is sufficiently large. This can, for example, be observed in case of the rightmost curve in Figure 2 above. Equilibrium remains a meta-stable state of the system.
In order to understand the possibility of a return to equilibrium, let us evaluate the conditions for lock-in in analytical terms. Lock-in into technology A, for example, occurs when it becomes more attractive for S-type agents to buy this technology despite their natural preference for technology B. From Table 1, we can see that this is the case when:
aS + snA > bS + snB
Thus:
snA - snB > bS - aS
(nA - nB) > (bS - aS)/s
From this result two further conclusions follow with respect to the possibility of preventing lock-in and then also with respect to the possibility of lock-out:
4. Given a parameter set, lock-in is a consequence of only the difference in the number of previous adopters (|nA - nB|). With increasing diffusion, this difference becomes smaller as a percentage of the total number of adopters (nA + nB). Consequently, the difference in market share becomes more difficult to assess by new arrivals who therefore tend to decide on the basis of their natural preferences and thus to prolong equilibrium. If one assumes reflexivity on the side of consumers, for example, as expressed by uncertainty about market shares among them, a window is created for prolonged periods of equilibrium.[Note 1]
5. If the network parameter of the loosing technology (e.g., technology B as the preference of S-type agents) is reduced to zero, the locked-in system reverts to equilibrium since the network-parameter s is part of the denominator in the above derived equation. The system is then necessarily "locked-out." Substantively, one may interpret this as an effect of setting the S-type agents free from the constraints of the previous lock-in, and thereby enabling them to return to their natural preferences.
The normative implication of this latter conclusion is counter-intuitive: in the case of a technology B that had to give way to the lock-in of a competing technology (A), a return to the market is not likely based on competition in terms of the existing network effects, but by dissolving them. This implies a radical innovation that sets the technology free from those contextual factors that were advantageous during the previous generation of the technology.
For example, the network externalities of the VHS system as a technology for VCR will disappear when video movies can be downloaded directly from the Internet. Customers can then be expected to use other storage media than a single brand of magnetic tape. Thus, paradoxically, a technology which has lost the competition should not be improved in terms of the current competition, since that was already lost. Changes in the institutional settings or, in other words, the political economy of the technology are conditional for a lock-out.
In summary, Arthur (1988) noted that equilibrium is enhanced if lock-ins can be postponed. We have now specified that this is dependent on the relation of the absolute difference between the number of adopters and the total number of adopters. Lock-outs can be provoked by introducing radical new technologies into a market with a sufficiently large number of adopters. Of course, competing technologies of the next generation can lock-in again. In that case, a next cycle is generated.
The normative implications are thus dependent on the stage of lock-in versus equilibrium. If one wishes to keep the system in equilibrium, one has to make the assessment of relative market shares difficult. As soon as there is an obvious winner, competitors will jump on the bandwagon at the expense of destroying previous competences. When a lock-in has occurred, the only other option is radical innovation affecting and involving the structural conditions of the technology.
Radical innovation implies that one has to break out of one's trajectory
at the price of "creative destruction" of in-house competences
and network externalities. In a corporate world, such a shift of trajectory
requires another set of institutional alliances. Since the needed restructuring
is radical, it is likely to be based on a cognitive reconstruction and
not on existing practices. One then abstracts from the current situation.
Lock-ins and Lock-outs
Bruckner et al. (1994) have shown — using a master equation approach — that successful innovation of this type remains highly improbable given a lock-in. In terms of evolutionary theorizing, a radical innovation requires tunneling of the trajectory through a so-called "separatrix" in the phase space; that is, one has to find another basin of attraction. An essential condition for this unlikely event is the creation of a niche in which the new technology can find sufficient applications so that it can withstand the competition on this basis.
A corporation may be able to create a niche in collaboration with a
government, or perhaps by aiming at specific user groups (Lundvall 1988;
Nelson 1993). A mechanism has to be brought into place that shields the
new technology from the effect of the "hyper-selective" environment
of the open market. This temporary shielding of the market leads almost
by definition to market segmentation. One can simulate this situation in
the Arthur-model by assuming not only two competing technologies, but also
two selection environments (see Table 3). For the moment, we can
disregard from the issue of whether these environments are different nation
states or market segments.
| technology A | technology B | |
| market C | AC | BC |
| market D | AD | BD |
Table 3
R- and S-type potential adopters of technologies A and
B
arrive randomly in selection environments C and D
Let us, for the sake of simplicity, assume that the parameter values are similar to those in the previous case. R-type and S-type adopters arrive randomly as before. The network effects in the two market segments (C and D) are initially identical. First, we will examine what happens when the choice between technology A and technology B is independent of whether adopters arrive in market C or market D. In other words, we introduce a second stochast and we evaluate the four possible combinations AC, AD, BC, and BD without any assumptions of deliberate and/or effective coupling between the respective technologies and market segments.
The code for this simulation is provided in Table 4 in a format similar to that of Table 2. Note that in line 730, one is able in principle to turn the printer on in order to make a quantitative assessment of the timelines which are produced. However, we limit the analysis in this study to a qualitative appreciation of the results.
| 10 INPUT N
20 SCREEN 11: WINDOW (-2, 0)-(N, 100): CLS 30 FOR J = 1 TO 10 40 LINE (-2, 50)-(N, 50): LINE (-2, 25)-(N, 25): LINE (-2, 75)-(N, 75) 50 RA = .8: RB = .2: SA = .2: SB = .8: s1 = .01: r1 = .01 51 RC = .8: RD = .2: SC = .2: SD = .8: s2 = .01: r2 = .01 52 NAC = 1: NAD = 1: NBC = 1: NBD = 1: NA = 2: NB = 2: NC = 2: ND = 2 60 RANDOMIZE TIMER 70 FOR I = 1 TO N 80 xx = RND 90 yy = RND 100 IF xx < .5 AND yy < .5 GOTO 200
200 returnA = RA + r1 * (NAC + NAD): returnB = RB + r1
* (NBC + NBD) 300 returnA = RA + r1 * (NAC + NAD): returnB = RB + r1
* (NBC + NBD) 400 returnA = SA + s1 * (NAC + NAD): returnB = SB + s1
* (NBC + NBD) 500 returnA = SA + s1 * (NAC + NAD): returnB = SB + s1
* (NBC + NBD) 600 IF returnA > returnB THEN NA = NA + 1 ELSE NB =
NB + 1 700 Y = NA + NB |
| Table 4 Extension of Arthur's (1988) model: two stochasts with cross-tabling |
The results of running the model as specified in Table 4 are
exhibited in Figure 3 for a single run. In other runs, the moment
of lock-in varies, but the pattern is essentially similar to that shown
in Figure 1. The system locks in, first, along one of the two dimensions
of, for example, technologies A and B, and only thereafter
and independently in the other dimension (in this case markets C
and D). In Figure 4, I anticipate the further discussion
below by exhibiting the result of adding a third dimension (E and
F) to this system. The system has now 23 = 8 options,
and the three bifurcations lock-in subsequently. The chance of lock-in,
of course, increases with the number of dimensions given the same parameter
values.
 |
 |
| Figure 3 Extension of the Arthur-model to two technologies and two markets |
Figure 4 Three stochasts, and therefore 23 options |
For analytical reasons, equilibrium remains an (unstable) option as before. The situation is not fundamentally different from the situation with a single source of randomness, since we have not yet accounted for the possibility of couplings in this model. The idea of sustaining a niche in the market, however, is based on the surplus value of a positive coupling of a specific technology with a market segment. Thus, one intends to capitalize on the combination of a technology and a temporarily protected environment as an interaction effect.
There are several ways to model such positive reinforcement using the
program in Table 4. For example, one may insert a line 220 to the
code after line 210, specifying that in the case of this combination the
corresponding network parameters (in this case, r1 and r2)
are increased with one promille (that is, r1 = r1 * 1.001
and r2 = r2 * 1.001) because these two parameters were selected.
(Analogously, one can then add a line 320 specifying: "r1 =
r1 * 1.001" and "s2 = s2 * 1.001,"
etc.) Alternatively, one may wish to add these conditions only after the
realizations of the corresponding combinations, that is, after lines
640, 650, 660, and 670, respectively. One might also wish to assume other
coupling mechanisms. However, the details of the specification do not really
matter for the overall effect: a positive interaction effect always enhances
lock-in in the case of two stochasts, as shown for a typical case in Figure
5. When two selectors are coupled in a model with this type of (positive)
interaction effect, lock-ins are enhanced significantly. The system is
expected to lock-in into one of the four options.
|
|
| Figure 5 Coupling of two stochastic processes enhances the lock- in |
The enforcement of the lock-in of a technology can be considered as a coevolution with a specific environment or also as the generation of a trajectory: the resulting system is developed using specific trade-offs in terms of both technologies and environments (Dosi 1982). The market is not only taken over by one of the two competing technologies (as in the previous case), but this winning technology is also captured within a specific environment.
Note the recursivity in the development. A fit may be generated, for
example, in terms of a dominant design at the level of a firm. The dominant
design captures the industry (Abernathy & Utterback 1978; Tushman &
Anderson 1986; Anderson & Tushman 1990). Once a technology is dominant,
the differentiation of market structures provides a potential mechanism
for the creation of niches in which stronger fits can be elaborated. For
example, the Airbus-300 series of the 1980s codified the design principles
of the Boeing-700 series, thereby turning the latter into the industry
standard (Frenken & Leydesdorff, forthcoming). The thus emerging regime
is expected to conquer the market by restructuring it.
The Triple Helix
Figures 6 and 7 provide examples of coupling in the case of three stochastics.
Whenever an order is imposed on the system only in the weakest sense —
for example, by declaring a single conditional relation between the returns
[Note 2] — the pattern of independent lock-ins can be completely disturbed.
Lock-in is still expected, but the effects tend to be global: all competing
combinations can be affected indirectly. In this case, the systems are
coupled algorithmically in dimensions other than those that can be observed
directly and consequently a complex dynamics is generated.
 |
 |
| Figure 6 A Triple Helix with small errors (30,000 adapters) |
Figure 7 Second example; similar run |
In Figure 6, we observe the lock-in of a technology/market combination
that was not initially leading. However, the initially dominant combination
is able to keep a considerable market share despite the extension to 30,000
adopters, as against 10,000 in the previous runs. Figure 7 exibits
a run in which the initially leading combination is negatively affected
by the final lock-in and then loses the competition.
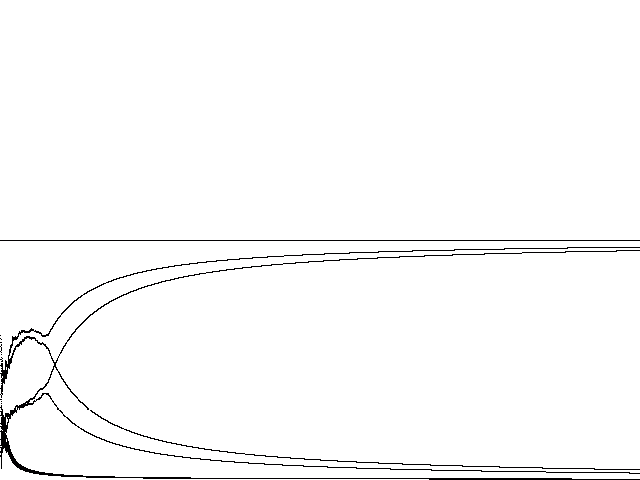 |
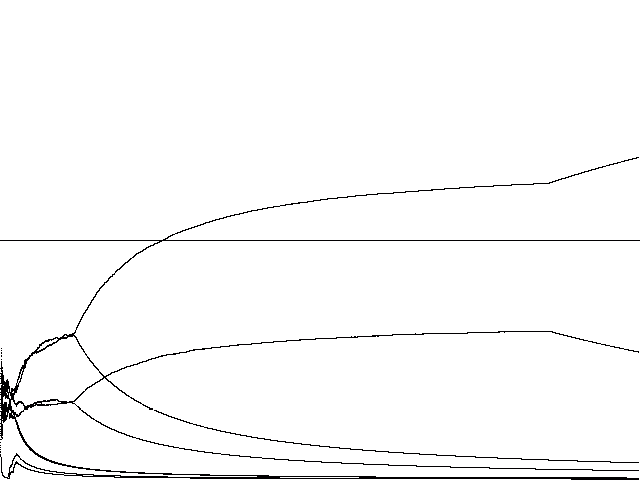 |
| Figure 8 Two winners in different suboptima (30,000 adapters) |
Figure 9 Two winners in different suboptima (30,000 adapters) |
Figures 8 and 9 provide examples of runs in which two different
combinations are locked-in. Because of the non-linearities introduced two
equilibria can be created in the case of three random, but partially coupled
dynamics. The possibility of multiple equilibria can be explained using
Kauffman's (1993) NK-model of random fitness landscapes (Frenken, this
issue).[Note 3] As Figure 9 illustrates, the configuration can
be meta-stable under this condition of continuous disturbances.
Conclusions
By extending a routine proposed by Arthur (1988 and 1989) for modelling a basic understanding of network effects in the case of competing technologies, it could be demonstrated that three interacting dynamics may generate highly unpredictable effects. Because of the negative (that is, selective) feedback loops involved, the risks of bringing an innovation process locally to an end should not be neglected. If, on the other hand, a technology fits into a lock-in, a trajectory is generated that can be expected to perform a "life"-cycle as long as it is not systematically disturbed by developments at the next-order level of the technological regime.
Before turning to the normative implications, let me recapitulate the argument. First, technologies and markets tend to couple along trajectories because of the contingencies and the historicities involved. These frictions generate operational uncertainties that enhance lock-in (Foray 1998). The resulting markets, however, are different from primitive markets in the sense that thereafter the markets are no longer elastic in terms of prices. Evolutionary economics has studied these rigidities in science-based production processes (e.g., Rosenberg 1976; Leydesdorff & Van den Besselaar, forthcoming). Technically, price/performance ratios and other sophisticated decision criteria tend to replace simple pricing as the selection mechanism (Teubal 1979; Lundvall 1988).
Trajectories compete recursively, but in a multi-dimensional phase-space of possible selections. Whereas corporations have been the main carriers of trajectories, state intervention has been a major agent for change in the phase-space of different trajectories (Leydesdorff & Etzkowitz 1996). The reflexive feedback codes the competition with another layer. Science and technology provide this code with legitimation. One reason for coding the feedback has been that without the additional layer of social organization monopoly would prevail in the long run - as a consequence of lock-in - and the system might not be sufficiently innovative. Analogously, the European Union is based on the assumption that it is possible to dissolve national lock-ins by adding another layer of networking with its own code.
While multi-national corporations have been able to take national differences as a source of variation for their selections, the internal differentiation of the bureaucracy in terms of supra-national, national, regional, and semi-government agencies has opened up a range of possible interactions in the third dimension of the triple helix. Since this interaction has increasingly been coded in political discourse - for example, in the case of Europe in terms of "the subsidiarity principle"- a regime comparable with those illustrated by the last simulations was generated (Frenken, this issue).
Although the development of a triple helix interaction can be traced back to the second half of the 19th century (e.g., Noble 1977; Rip & Van den Belt 1987), the codification of the network mode as a regime of university-industry-government communications is of rather recent date (Leydesdorff 1997a). The expansion of the higher-education sector during the 20th century has provided the social system with an operational reservoir of reflexive knowledge (e.g., Parsons & Platt 1973). The globalized regime of a triple helix adds a degree of freedom to the observable systems: in the complex negotiations one is able to select among the trajectories that -from a different perspective- can be considered as the institutional constraints. The contextual embeddedness of the innovation process can further be overcome by using virtual dimensions (Nowak & Grantham, this issue); the "laboratory model of innovation" can gradually be supplemented with a "desk top model" using representations (Kaghan & Barnett 1997; Gibbons et al. 1994).
Trajectories are based on contingent co-evolutions between two of the three helices. For example, trajectories are expected to emerge in the interaction between technologies and markets. National governments and large-scale technologies have sometimes been locked-in, as in the former Soviet economies when market forces were lamed. Lock-ins between nation states and market forces are typical of systems which are not (yet) science-based. The triple helix regime operates in terms of recursive selections. Since one selects on the observables reflexively, the mode of operation is transient or "Mode-2" (Gibbons et al. 1994).
The overlay operates by reflexively selecting from the observables on
the basis of expectations that are socially distributed. Expectations can
be improved when they are made the subject of systematic research. Thus,
expectations and their interactions are increasingly the basis of social
order in a knowledge-based economy. This overlay continuously reshapes
the observable institutions in university-industry-government relations,
yet in a network mode.
Normative implications
When the system has become so complex that it can be analyzed and appreciated in terms of a triple helix, local action obtains a different meaning. Local action is provided with meaning at the level of a specific trajectory, while its effectiveness is based on a non-linear interaction. The network system that operates in terms of expectations is more volatile then its retention mechanism. Paradoxically, the chances of success of policies at the intended locations are low; unintended consequences can be expected to prevail.
The complex system remains in need of disturbances by local action since it operates by selecting on them. Thus, active policy-making is a necessary ingredient of a triple helix system, but the fruits of the efforts are rather unpredictable, since other sources of variation may be introduced and the trajectories can be expected to be disturbed. The disturbance terms contain the potential for innovation if they can be sustained. Further development is beyond control because it is based on selections at other ends.
This argument leads to the conclusion that in order to be effective, policy-making should be reflexive in several respects. Which system of reference is being disturbed, and how complex are these systems from a dynamic perspective? As long as the system of reference can be considered as a local trajectory, concrete barriers to its further development can be identified and perhaps removed. One may wish to call this the "industrial model." Control remains possible, effects are identifiable, and consequences can thus be evaluated meaningfully from within local frames of reference. For example, one may wish to stimulate or even to force the development of more environmentally friendly technologies as long as "the environment" can be defined unambiguously.
As soon as the system under study (for example, a science-technology like biotechnology) has evolved into a global regime, other sources of uncertainty begin to play a role. Active policies may be productive in dimensions of the complex system other than the ones taken in focus. Of course, one can try to trade-off between different objectives, but the results remain predictably sub-optimal (cf. Callon 1998). Others may unexpectedly be able to realize considerably improved results by focusing on possible recombinations. The global system is not expected to reward local policy-makers fairly, yet sustained disturbance is essential for the dynamics of this system.
This is not a plea for "laissez faire, laissez aller." However, it is an argument against an engineering model of society and S&T policies. The relevant environments can be hypothesized and therefore the development is knowledge-intensive. The global system can only advance in so far as local stabilizations can be subjected to further selections. To this end, niches have to be nurtured and regions developed. The more precise (that is, reflexive) the signals from institutional actors can be, the more likely one will be able to participate in the system's further development. The innovators have to place themselves reflexively within the innovation process.
A competitive advantage (based, for example, on engineering) is a necessary but not a sufficient condition for participation. Without further provisions for future feedback loops, the innovators cannot expect to be rewarded. In general, the innovated systems benefit from innovations, and not the innovators. From an evolutionary perspective, a locally progressive development is always endangered. In terms of policy analysis, one should not focus only on positive achievements like pilot projects, but on the possibilities for sustaining and using the new developments further (under selection pressure) and on organizing institutional retention (Leydesdorff 1997b).
Innovation and invention are actor categories; innovativeness and resilience are crucial to an understanding of the (selecting) system's operation. At the level of the communication system, the specification of dimensions potentially relevant for future developments assumes a theoretical reflection on possible developments. Thus, the loop of a cultural evolution based on scientific reconstructions and discursive reasoning can be considered "locked-in" within a knowledge-based economy.
return to home page
Notes
* The author is grateful for contributions to this paper by Henry Etzkowitz, Koen Frenken, and Peter van den Besselaar. I acknowledge partial funding by the European Commission, TSER project SOE1-DT97-1060: "The Self-organization of the European Information Society."
[1] Such effects can be shown in the simulations. For example, if one changes the instructions in lines 110 and 150 (in Table 2) from "IF RETURNA > RETURN B THEN ...." into "IF RETURNA > 0.95 * RETURNB THEN ... (and vice versa), lock-ins seldom occur given the above values for network parameters. For example, if agents are willing to pay up to 5% more for their preferred product, equilibrium can be maintained given the parameter values in Table 2 (Leydesdorff & Van den Besselaar 1998).
[2] The simulations in this section are based on introducing a single transitive relation into what corresponds to line 640 in Table 4, but then for the case of three stochasts. Instead of "IF returnA > returnB AND returnC > returnD AND returnE > returnF", the specification was "IF returnA > returnB AND returnC > returnE AND returnE >returnF", thus creating a hierarchical relation between "returnC > returnE > returnF" as a condition. Similar results could be produced by introducing other hierarchies.
[3] In the case of eight (23) possible genotypes, more than a single local optimum is possible in a fitness landscape for N = 3 (Kauffman 1993, at pp. 42 f.). In general, the number of local optima in a random fitness landscape can be (2N) / (N + 1) at the maximum (Kauffman 1995, pp. 166 ff.). The figures depicted here can be considered as possible uphill walks in this fitness landscape (cf. Frenken, this issue).
return to home page
References
Abernathy, W. J. & J. Utterback (1978). "Patterns of Industrial Innovation," Technology Review 50, 41-47.
Anderson, P. and M. L. Tushman (1990). "Technological discontinuities and dominant designs: a cyclical model of technological change," Administrative Science Quarterly 35, 604-33.
Arthur, W. Brian (1988). "Competing technologies." Pp. 590-607 in: G. Dosi, C. Freeman, R. Nelson, G. Silverberg, and L. Soete (Eds.), Technical Change and Economic Theory. London: Pinter.
Arthur, W. Brian (1989). "Competing Technologies, Increasing Returns, and Lock-In by Historical Events," Economic Journal 99, 116-31.
Biggiero, Lucio (1998). "Italian industrial districts: a Triple Helix pattern of problem solving," Industry & Higher Education 12, 227-34.
Bruckner, Eberhard, Werner Ebeling, Miguel A. Jiménez Montaño, and Andrea Scharnhorst (1994). "Hyperselection and Innovation Described by a Stochastic Model of Technological Evolution." Pp. 79-90 in: Leydesdorff & Van den Besselaar (1994).
Bruckner, Eberhard, Werner Ebeling, Miguel A. Jiménez Montaño, and Andrea Scharnhorst (1996). "Nonlinar stochastic effects of substitution — an evolutionary approach," Journal of Evolutionary Economics 6, 1-30.
Callon, Michel (1998). "An essay on framing and overflowing: economic externalities revisited by sociology." Pp. 244-69 in: Michel Callon (Ed.), The Laws of the Market. Oxford and Malden, MA: Blackwell.
Constant II, E.W. (1980). The Origins of the Turbojet Revolution (Baltimore and London: Johns Hopkins University Press).
David, Paul A. (1985). "Clio and the Economics of QWERTY", American Economic Review 75, no. 2, 332-37.
David, Paul A., and Dominique Foray (1994). "Dynamics of Competitive Technology Diffusion Through Local Network Structures: The Case of EDI Document Standards." Pp. 63-78 in Leydesdorff & Van den Besselaar (1994).
Dosi, Giovanni (1982). "Technological Paradigms and Technological Trajectories: A Suggested Interpretation of the Determinants and Directions of Technical Change," Research Policy 11, 147-62.
Etzkowitz, Henry, and Loet Leydesdorff (Eds.) (1997). Universities and the Global Knowledge Economy: A Triple Helix of University-Industry-Government Relations. London: Cassell.
Foray, Dominique (1998). Errors and Mistakes in Technological Systems: From Potential Regret to Path Dependent Inefficiency. Pp. 217-239 in: Jacques Lesourne and André Orléan (Eds.), Advance in Self-Organization and Evolutionary Economics. London, etc.: Economica.
Frenken, Koen (this issue). "A Complexity Approach to Innovation Networks. The Case of the Aircraft Industry (1909-1997)." Paper presented at the Second Triple Helix Conference, State University of New York at Purchase, January 1998.
Frenken, Koen and Loet Leydesdorff (forthcoming), Scaling Trajectories in Civil Aircraft (1913-1970), Research Policy.
Kaghan, William and Gerald B. Barnett, "The Desktop Model of Innovation in Digital Media." Pp. 71-81 in: Etzkowitz & Leydesdorff (1997).
Kampmann, Christian, Christian Haxholdt, Erik Mosekilde, and John D. Sterman (1994). "Entrainment in a Disaggregated Long-Wave Model." Pp. 109-24 in: Leydesdorff & Van den Besselaar (1994).
Kauffman, Stuart A. (1993). The Origins of Order: Self-Organization and Selection in Evolution. Oxford: Oxford University Press.
Kauffman, Stuart A. (1995). At Home in the Universe. New York/Oxford: Oxford University Press.
Leydesdorff, Loet (1994). "The Evolution of Communication Systems," Int. J. Systems Research and Information Science 6, 219-30.
Leydesdorff, Loet (1997a). "The New Communication Regime of University- Industry-Government Relations," Pp. 106-117 in: Etzkowitz & Leydesdorff (1997).
Leydesdorff, Loet (1997b). "Sustainable Technological Developments and Second-order Cybernetics," Technology Analysis & Strategic Management 9, 329-41.
Leydesdorff, Loet & Henry Etzkowitz (1996). "Emergence of a Triple Helix of University-Industry-Government Relations," Science and Public Policy 23, 279-86.
Leydesdorff, Loet & Henry Etzkowitz (1998a). "The Triple Helix as a model for innovation studies," Science and Public Policy 25, 195-203.
Leydesdorff, Loet & Henry Etzkowitz (1998b). "The Triple Helix of Innovation," Science and Public Policy 25 (6), forthcoming..
Leydesdorff, Loet & Peter Van den Besselaar (Eds.) (1994). Evolutionary Economics and Chaos Theory: New directions in technology studies. London: Pinter.
Leydesdorff, Loet & Peter Van den Besselaar (1997). "Competing Technologies: Disturbance, Selection, and the Possibilities of Lock-in." Pp. 60-64 in: Daniel M. Dubois (Ed.), Computing Anticipatory Systems. Liège: Chaos.
Leydesdorff, Loet and Peter van den Besselaar (1998). "Competing Technologies: Lock-ins and Lock-outs." Pp. 309-23 in: Daniel M. Dubois (Ed.), Computing Anticipatory Systems, Proceedings of the American Institute of Physics 437. Woodbury, NY: American Institute of Physics.
Leydesdorff, Loet and Peter Van den Besselaar (1999), Technological Development and Factor Substitution in a Non-linear Model, Journal of Social and Evolutionary Systems 21 (1998, No. 2; forthcoming).
Luhmann, Niklas (1984). Soziale Systeme. Grundriß einer allgemeinen Theorie. Frankfurt a. M.: Suhrkamp. [Social Systems. Stanford: Stanford University Press, 1995.]
Lundvall, Bengt-Åke (1988). "National Systems of Innovation." Pp. 349-69 in: G. Dosi, C. Freeman, R. Nelson, G. Silverberg, and L. Soete (Eds.), Technical Change and Economic Theory. London: Pinter.
McKelvey, Maureen D. (1997). "Emerging Environments in Biotechnology." Pp. 60-70 in: Henry Etzkowitz & Loet Leydesdorff (Eds.), Universities and the Global Knowledge Economy: A Triple Helix of University-Industry-Government Relations. London: Cassell Academic.
Mowery, David C. and Nathan Rosenberg (1981). "Technical change in the commercial aircraft industry, 1925-1975," Technological Forecasting and Social Change 20, 347-58.
Nelson, Richard R. (Ed.), (1993). National Innovation Systems: A comparative study. New York, Oxford University Press.
Nelson, Richard R. (1994). "Economic Growth via the Coevolution of Technology and Institutions." Pp. 21-32 in: Leydesdorff & Van den Besselaar (1994).
Nelson, Richard R. and Sidney G. Winter (1977). "In search of useful theory of innovation," Research Policy 6, 36-76.
Nelson, Richard R. and Sidney G. Winter (1982). An Evolutionary Theory of Economic Change. Cambridge, MA: Belknap Press.
Noble, David (1977). America by Design. New York: Knopf.
Nowak, Michael J. and Charles E. Grantham (1999). "The Virtual Incubator: Managing Human Capital in the Software Industry," Research Policy (this issue).
Parsons, Talcott, and Gerald M. Platt (1973). The American University. Cambridge, MA: Harvard University Press.
Rosenberg, Nathan (1976). Perspectives on Technology. Cambridge, MA: Cambridge University Press.
Simon, Herbert A. (1969). The Sciences of the Artificial. Cambridge, MA/ London: MIT Press.
Teubal, Morris (1979). "On User Needs and Need Determination. Aspects of a Theory of Technological Innovation." Pp. 266-89 in: M. J. Baker (Ed.), Industrial Innovation. Technology, Policy and Diffusion. London: Macmillan Press.
Tushman, M. L., and Philip W. Anderson (1986). "Technological Discontinuities and Organizational Environments," Administrative Science Quarterly 31, 436-65.
Van den Belt, Henk, and Arie Rip (1987). "The Nelson-Winter-Dosi model and synthetic dye chemistry." Pp 135-58 in: Wiebe Bijker, T. P. Hughes, and T. Pinch (Eds.) (1987). The Social Construction of Technological Systems. Cambridge, MA: MIT.
return to Leydesdorff's
home page