Introduction
While there has been debate about whether innovations are integrated into systems nationally, regionally, or sectorially focusing on specific technologies
such as biotechnology [3, 4], the systemic character of innovation and
technological development itself is hardly contested since Dosi [5]. Unlike the
neo-classical economics approach of comparative statics, with a focus on market
forces creating equilibria at each moment in time, evolutionary economists have emphasized the historical character of innovation processes [6, 7, 8, 9]. According to Schumpeter
[10] and Nelson & Winter [8, 9], market equilibria are disturbed by innovations made possible by technological developments over time. The recurrence of this disturbance
term may lead to rigidities in the market along trajectories [5, 7]. Evolutionary
economics has, however, acknowledged the role of market demand influencing how a
technological paradigm emerges and develops as well [11, 12].
Selection by the market and stabilization along a
technological trajectory over time may lead to the development of a technological
paradigm that can be locked-in. Lock-in of technologies into a paradigm has
been argued to be potentially sub-optimal [13, 14, cf. 15]. For a lock-in to
emerge and transform (stabilize) into a ‘natural trajectory’ or ‘technological
regime’ other relevant selection mechanisms need to have reinforced the
selection [9: pp. 258f.]. Negative reinforcement, however, is also possible and
empirically observable: not all technologies are permanently locked-in into a
trajectory [16, 17, 18, 19].
Lock-ins between two subdynamics in a process of mutual
shaping can discourage or even prevent new developments. For example, when the
market is reinforced by network externalities among previous adopters, the development of a new generation of technologies can be irrelevant to the techno-economic system
which prevails. A third selection mechanism impinging on decision-making about
relevant combinations at the interfaces between supply-side opportunities and
demand-side expectations [20] may then upset a locked-in trajectory. In the case
of three relevant selection environments interacting a break-out from a lock-in
can also be modeled.
In the formal model developed in this paper, we elaborate substantially on the
work of Arthur and others.
Like markets and technologies, markets and political
decision-making processes can co-evolve along trajectories. Analogously,
technologies and political decision-making processes can also be locked-in into
state apparatuses. The three different selection mechanisms are equivalent a
priori.
Which technology will be locked-in emerges from the interaction among the three
subsystems in potentially unstable conditions, possibly independently of the
inherent qualities of the competing technologies.
There need thus not be a decision by a specific actor in the system for lock-in
or break-out to occur, but rather a non-linear dynamics at the systems level can generate these effects [29].
The paper proceeds as follows. Section 1 sets out the
classical Arthur framework as an important backdrop for our formal modeling and
policy recommendations. Especially Arthur’s [2] implicit assumption, not given
sufficient recognition, that lock-in results from two selection environments
moving in lockstep is further developed in this paper. Section 2 shows how
interaction with a third selection environment can be modeled. Section 3 then
derives conditions for break-out from a lock-in that Section 4 further
elaborates into options for policy makers in governments and strategy makers in
firms.
1. Arthur’s Model of Lock-in
Brian Arthur [1, 2] specified the mechanism for lock-in in
the case of two competing technologies with randomly arriving adopters following
their given preferences in a market with marginally increasing returns. Each
adopter changes the situation for adopters thereafter, as it can be more
attractive to buy a brand or type of product that is common in the market-place
than one that is rare. Such a market in this sense is self-organized. The
recursive mechanism in the aggregation of “network externalities” leads necessarily,
according to Arthur, to a lock-in in the long run. Arthur used the example of
the VCR: if one particular standard (e.g., VHS rather than Betamax) is
increasingly accepted, one passes a point of “no return” and soon video-stores will only have tapes on their shelves for the dominant type of video recorder only.
In Arthur’s (1988) formal model two types of agents, R and S,
with different “natural inclinations” towards two competing technologies, A
and B, are present. In Table 1, aR represents the natural
preference of R-type agents towards technology A, and bR
their (in this case, lower) inclination towards B: aR > bR.
Analogously, one can attribute parameters aS and bS to
S-type agents (bS > aS). The network effects of
adoption (r and s) are modeled as coefficients to the number of
previous adopters of the respective technologies (nA and nB).
|
|
Technology A
|
Technology B
|
|
R-Agent
|
aR + rnA
|
bR + rnB
|
|
S-Agent
|
aS + snA
|
bS + snB
|
Table
1: Returns for agents R and S to
adopting technology A or B, given nA and nB
previous
adopters
of A and B [2: 118]
The values of the cells in Table 1 indicate the return that
an agent receives for adoption of the respective technology. In addition to the
satisfaction of obtaining the technology of one’s choice—that is, following a
natural inclination—the attraction of a technology is increased by previous adopters with a term r for each R-type agent, and s for S-type agents. If
R-type and S-type agents arrive on the market randomly, the theory of random
walks predicts that competition will eventually lead to a lock-in on either
side (A or B) due to these positive feedback loops.
For example, agent S would prefer to buy technology B
(since bS > aS), but when the total
return for buying technology A (aS + snA)
is larger than the return for buying technology B (bS + snB)
this agent will nevertheless buy technology A. In formula format, the
condition for this lock-in is:
aS + snA
> bS + snB (1)
The condition for the lock-in into the other technology can
be specified, mutatis mutandis.
The model is elegant and can easily be programmed as a
computer simulation. Using simulations, it can be shown that lock-ins are
robust against changes in parameter values by orders of magnitude [29]. Once in
place, a lock-in will not normally lead to a break-out to the other technology,
or to a return to a competitive balance between the two technologies. Strong
reduction of the network effect for the winning technology (in our case, r)
or, alternatively, enhancement of the network effect of the losing technology
(in this case, s), even by orders of magnitude, is not likely to change a
locked-in configuration.
Simulation results presented in Figure 1 show that if one
forces a break-out by further increasing (or decreasing) parameter values by orders of magnitude, the replacement pattern reverts to the curve for lock-in of the other
technology. In Figure 1, substitution was forced when technology A
was the previously locked-in technology. These rapid, but ordered substitution
processes have, for example, been noted by [30] in seventeen cases of
technological substitution. Their finding was that the rate of substitution in
all the cases, once begun, did not change throughout its history, but was to be
considered as a systems property. Our simulations confirm their findings.
|
market share of techn. A
↑
50%
|

|
|
|
Time →
|
|
Figure 1: Forcing technological break-out from a lock-in and
possible return to equilibrium (20,000 adopters) [29, p.316].
|
In summary, the rate of adoption of a specific technology is
not proportional to historical advancements in the technology, but is
determined by an evolutionary mechanism underlying substitution. The dynamics
are a result of interaction effects among dimensions at the systems level. The dissolution of a lock-in is, in other words, not determined by the emergence of a new
and superior technology, but by the balance between the interlocking
networks of markets and the attractiveness of the technologies for users [31].
Co-evolving sub-systems may thus suppress related sub-dynamics [32].
As Figure 1 indicates (rightmost curve), there is the
possibility of a return to a competitive balance between technologies, but only
if the market is sufficiently large. Changes in the parameter values can sometimes cause a return to balance or a cascading all the way to a lock-in into the
other technology. We would like, however, to suggest that there is a wider set
of circumstances that allow for a break-out from a lock-in, and that the
process of break-out is in need of a better conceptual understanding.
2. Three Selection
Environments
The development of a single system x in an environment can be modeled using the logistic equation as follows:
 ; 0 < x <
1 (2)
; 0 < x <
1 (2)
In biology, this equation has been used to model the growth
of a population. The feedback term (1 – xt) inhibits
the further growth of this system as the value of xt
increases over time.
In the case of a techno-economic system, the technological development generates variation on the basis of the previous state of the system (modeled above as axt), but this variation is selected by a market environment.
For populations or technologies which compete, one can
generalize the logistic equation to the so-called Lotka-Volterra equation in
which competition coefficients (α) are added to the selection mechanisms [37;
38; 39; 40, p.98). In both the logistic equation and the Lotka-Volterra
equation, selection is represented by a feedback term. This feedback is modeled
as k – αx in the case of Lotka-Volterra. Assuming unity of the
parameters and without loss of generality it can be modeled as (1 – x).
Two selections operating on a technological variation v (defined above as axt) therefore result in the following quadratic expression for the
resulting selection environment:
f ( x ) = v (1 – x )
( 1 – x )
= v (x2
– 2 x + 1) ( 3 )
This selection environment no longer operates homogenously,
and can be represented as a system with two selections that stabilize at the
minimum of the quadratic curve (Figure 2a, left-hand side). When this minimum
is extended along the time dimension, a valley is shaped in which the system develops along a trajectory [41, 42]. Emerging rigidities then increasingly structure a system [43].
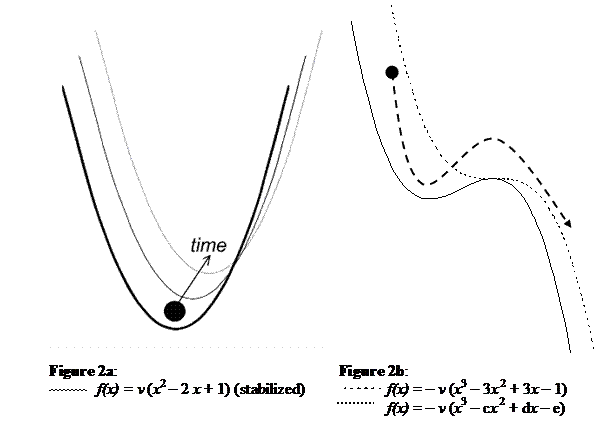
One may add another selection term to the equation, leading,
analogously, to:
f(x) = v (1 – x) ( 1 – x) ( 1 – x)
= – v (x3 – 3 x2 + 3 x – 1) (4)
This is represented in Figure 2b. As long as the different
selection mechanisms operate synchronously, with the same parameters, a saddle
point will emerge (dotted line in Figure 2b). Such a system contains a single (natural)
trajectory or regime. The drawn line in Figure 2b shows the configuration
resulting when the different selection mechanisms operate with dissimilar
parameter values. In this (more general) case the cubic curve shows both a
maximum and a minimum.
At the minimum, the techno-economic system is stabilized,
but at the maximum a bifurcation can be induced: the system can go left to the relatively stable (local) minimum. If the system goes to the right, the regime will cascade along another
trajectory, locking-in into a technological standard more globally. A system may
remain stable at the minimum, but the possibility of information entering the
system and upsetting the relatively stable (local) configuration may tend to move the system towards a global lock-in. One can also express this as the transition from a local
trajectory to a global regime [5]. The local optimum can be considered a niche
in which the technology may develop momentum to reach the maximum whereupon it
may lock-in at the level of the global market [44, 18]. (We will model this in
the next section as a bifurcation.) A niche where two selection enviroments
co-evolve may be more or less robust to an upset from a third environment.
The sign of the equations merits attention. Equation 3 had a
positive sign, and consequently the hyperbola in Figure 2a showed a minimum. If
another sub-dynamics comes into play, this sign is reversed (Equation 4): this
inversion cannot be endogenous to only two co-evolving selection
mechanisms which stabilized the system. A third selection mechanism needs to
come into play, a mechanism that either can reinforce the prevailing equilibrium (Figure 3b), or that can invert the sign and make the system susceptible to
bifurcation (Figure 3a).
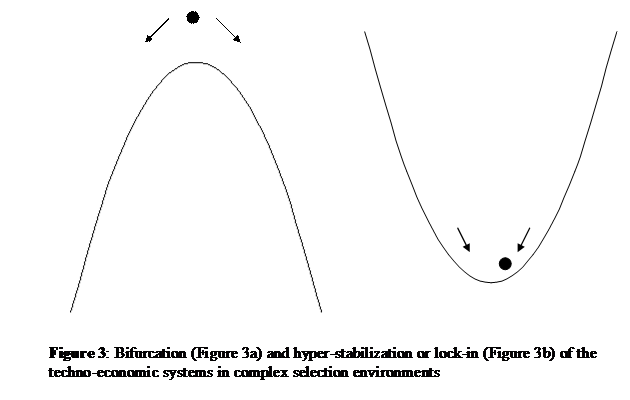
Figure 3a can be appreciated as a market with increasing
marginal returns forcing a system in one of two directions, as, e.g., in
Arthur’s [1] case of information and communication technologies. Increasing
marginal returns leads to a bifurcation as the system at the vertex of the hyperbole is vulnerable to the smallest of effects and will be led to a lock-in on
either side. A newly emerging situation is thereafter hyper-stable due to the
co-evolution between two sub-dynamics: a technology is locked-in, as in Figure
3b.
3. Lock-in and Break-out
Sub-optimal conditions due to a technology that is locked-in
into a sub-optimal trajectory is a well-known, though debated, phenomenon in
technological development [13, 14, 15]. The QWERTY keyboard, for example, was
invented in order to prevent jamming of the keys in the case of mechanical
typewriting. For various reasons (e.g., network externalities and learning curves; [6]), the subsequent lock-in could not be reversed after the conditions for this
technological fix of the jamming problem had disappeared. Although the use of
the QWERTY keyboard in the case of an electronic computer is sub-optimal,
attempts to reverse the prevailing lock-in have failed hitherto.[10]
Studies and models of lock-in have focused on the market (consumption)
side or on the technology (production) side, rather than on the interaction
between these two sub-dynamics. Under the neo-classical economic assumptions of
free competition and open markets, these two sub-dynamics are distinguished as
analytically independent, that is, as market clearing and technological innovation. Shifts along the production function due to changing factor prices are distinguished
from changes of the production function towards the origin due to technological
progress [10, 46].
Unlike the neo-classical framework, the perspective of evolutionary economics initially explicitly addressed the two sub-dynamics of trajectory
formation and selection environments as the subjects of theorizing [8, 9]. The
feedback terms were recognized by Nelson & Winter, but provisionally black-boxed [8, p. 49]. In their model, trajectory formation—specific organization over time—is induced by the interaction of relevant environments and resources in entrepreneurial
practices (e.g., routines). Entrepreneurial practices were considered as the
“natural” operators of the economic system [47]. Alternative yet largely
compatible explanations have focused on how trajectories form in terms of
dominant designs [e.g., 28, 48, 49, 50]. The mechanism of lock-in provides a formal model of the emergence of such a dominant design.
Break-out from a lock-in is possible, in practice as well as
in theory, as noted earlier in this article. Arthur [1, 2] showed that
potential adopters of a certain technology take the number of previous adopters of competing technologies into account when choosing, even though they may have
particular (given) preferences for a technologies. Lock-in can then not be avoided once an adoption threshold is passed. Unlocking of a lock-in can be considered in a more
comprehensive, formal manner, however, rather than in an ad hoc one. An
additional, third context that becomes relevant as another selection
environment may interact with the two co-evolving environments. The interaction
among three such selection environments can be modeled formally.
In the case of three interacting sources of variance a
complex regime can be expected to emerge. Recombination of three sub-dynamics
may generate various types of chaotic behavior [51, 52, 53]. Complex dynamics
of three sources of variation can generate lock-ins between two of the sources only
if the third context is stable and compatible with the others. This observation
is consistent with Kauffman’s NK-model [54, 55]. Dynamically, however, the
third selection mechanism may erode previously existing rigidities [56]. Return
to a competitive balance may be triggered by a historical event such as the advent of radically new technologies, possibly from a different technological
or market context [57]. Such historical events are, of course, exogenous to
evolutionary modeling. Modeling of a third selection environment implies,
however, that return to competitive balance can also be endogenized into the (evolutionary) model [58].
The problem of how a tight coupling between dynamics can be
dissolved can be modeled as reaction-diffusion dynamics which have been
elaborated in the natural sciences [59, 60, 61, pp. 182ff.].
If two systems are tightly coupled (as in a co-evolution; see Figure 5), a
simple coupling mechanism can, for example, be specified by the following
differential equations:
dx1/dt = – ax1
+ D(x1 – x2) + S (5a)
dx2/dt = – ax2
+ D(x2 – x1) + S (5b)
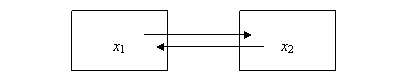
Figure 5: Two coupled processes [61, p.183].
Let us assume that x is produced in both compartments
at a constant and equal rate S. The parameter a represents the
decay of x; D is the diffusion constant across the interface.
(For the sake of simplicity, these parameters are assumed to be equal on both
sides.) The diffusion is asymmetrical depending on the concentrations of x1
and x2 in the two compartments. This system of
equations provides values for the steady state at:
x1* = x2*
= S / a (6)
The concentrations of x in the two environments are
then equal, the system is homogeneous. The operational stability of the system,
however, is determined in general by the eigenvalues of the matrix of the
coefficients of x1 and x2 in Equations 5a
and 5b. This matrix is:
The two eigenvalues of this system are:
λ 1 = – a; λ 2
= 2D – a (7)
While the first eigenvalue is always negative (λ1 = – a), the second can become positive if D > a/2. Thus, if
diffusion of x to the other system becomes more important than the flux
in the production process (divided by two), a positive and a negative eigenvalue coexist. The system then becomes unstable because a saddle point is
generated in the phase diagram (as in Figure 2b). Any deviation from
homogeneity will then be amplified, and the system can go through a phase transition,
changing the dynamics of the system irreversibly; for example, locking-into a
single particular technology.
In the case of two previously coupled dynamics, the
bifurcation leads to a polarization, that is, a situation in which all the
materials are either in the one cell or the other. Which sub-dynamic will prevail depends on the initial (and potentially random) deviation from homogeneity, possibly provided by the third environment. This more abstract mechanism explains both lock-in and break-out.
Lock-in into either Technology A or Technology B as discussed in
the previous section, can be triggered by a random event in a system which has
become meta-stable (see Figure 3a above). Break-out can be caused by the
increasing diffusion dynamics within a firmly coupled, and therefore locked-in,
system. As the diffusion parameter D increases, the previously existing
co-evolution may become endogenously unstable [cf. 62]. The trajectory along
which the locked-in system develops drives it to increasing diffusion of the
technology, and therefore, paradoxically, in so doing, generates the erosion of
the very conditions of the lock-in. The next-order globalizing system functions
as an attractor [63].
4. Conditions for Break-out From Lock-in
To understand the possibility of a return to a competitive
balance, consider the analytical conditions for the lock-in specified in Eq. 1.
Lock-in into technology A, for example, occurs when it becomes more
attractive for S-type agents to buy this technology despite their natural
preference for technology B. From Table 1 we derived Eq. 1 which
specifies that a lock-in is possible if [2: 120f.]:
aS + snA
> bS + snB (1)
Thus:
snA - snB
> bS - aS
(nA - nB)
> (bS - aS)/s (8)
As we will develop below, from this follow suggestions,
first, for preventing a lock-in, and, second, for a break-out from a lock-in,
as a third selection environment comes into play disturbing the co-evolution of the two interlocked selection environments.
This elaboration of the model provides certain key insights
that can inform both government policy
and strategic decision making by firms. Given values for the parameters of
natural inclinations and network effects, lock-in is a consequence of the
difference in the number of previous adopters for two competing technologies.
This difference is (nA - nB) if technology A is
the leading technology, and (nB - nA) in the opposite
case. With increasing diffusion, the difference |nA - nB|
becomes smaller as a percentage of the total number of adopters (nA
+ nB). In the case of large market shares for both technologies, the
difference in market share is more difficult to assess for newly arriving
consumers, and they will be more likely to decide on the basis of their natural
preferences and thus to prolong competitive balance between the technologies.
In other words, lock-in is easier to prevent in larger markets, and, paradoxically, is more likely to occur in the early stages of new
technological developments. If a player such as a government wants to maintain
a competitive balance between rivaling technologies, it will need to step in
strategically early on in the game, for example, by ostensibly buying the
technology that may appear to be loosing. There are, of course, other ways in
which governments can enlarge markets for a technology. Opening up markets
geographically or allowing technologies to be used for more and different
purposes are among them.
Firms as strategic agents have an interest in preventing
lock-in, forcing a break-out, or ensuring competitive balance as well. Our
model can thus also be considered as a contribution to analyzing competitive relations
between firms. Examples of this are airline companies buying airplanes from
both Airbus and Boeing, or local and national governments buying the Linux
operating system to counter the dominance of the Windows OS in the private sector. Neither of these buying parties would like one supplier to be able to monopolize
the market based on the technical characteristics of the products it offers and
may be willing to accept technically inferior or more expensive goods from
alternative suppliers to prevent lock-in as well as what economists call
hold-up [65]. Alternatively, an actor such as a government may prevent knowledge about the relative market shares from becoming available to adopters, to the
extent possible. The way in which information about a market becomes available
can have profound effects on their functioning [66]. By keeping alternative technologies in the race until markets are well established, lock-in can be postponed or even prevented [67]. Since competitors can be expected to jump on the bandwagon of a technology
that gets locked-in, even to the extent of destroying previous competences [68],
this may prevent undue disappearance of competing technologies and the
competences to further develop them for future use possibly in a different
context [18].
This happened, for example, to the V2000 and the Betamax
video systems competing with the VHS system sponsored by JVC and Matsushita. The
products offered by Philips and Sony, respectively, while technically superior,
were not accepted in the market as the locked-in dominant design. Philips and
Sony both abandoned this area of technical expertise altogether. The competition
between different standards for video recording is an appealing case that is
much referred to, but it is also a case with a number of additional angles to
it [30]. VHS became the dominant technology during the early 1980s and well
into 1990s, even though technically it was not superior. The CD did not change
this, as video material could not be recorded on it. The DVD, however, became increasingly relevant as an alternative, but this did not mean that the lock-in was
immediately broken. A prevailing system can be resilient. After a while, however, when the DVD-share grew independently for other reasons (e.g., due to its superior data
storage characteristic), the system tilted and a substitution process generated
an cascading away from the VHS towards an entirely new system dynamics. In
terms of our modeling, this should be seen as a grown market, affecting the
value of D in Equation 5 above. The newly emerging lock-in can be
expected to follow the curve of the alternative technology (Figure 1). In terms
of the visualization of Figure 2b, the system moves over the hilltop and
cascades into a new basin of attraction.
When a lock-in has occurred, the only other option may
sometimes be a radical innovation affecting the structural (selection)
conditions for the technology. The relevant contexts of the technology need to be
changed in order to induce a break-out. Changes at the level of a system can
also occur when a new technology that has more pervasive product
characteristics becomes available. DVDs, for example, can be considered as a
systems innovation when compared with VCRs [41] as they can be used for both video recording and data storage to serve a market much larger than the previous one [69]. Radical innovation implies that one breaks out of one’s trajectory, ‘creatively
destroying’ in-house competencies and network externalities.
The right-hand side of Equation 8 suggests that, if the
network parameter s of the losing technology (e.g., technology B
as the preference of S-type agents) is reduced to zero, the locked-in
system is necessarily “unlocked” and reverts to a competitive balance between the rivaling technologies. When s = 0, S-type agents are free
from the constraints of a previous lock-in, and are thereby enabled to return
to their natural preference (bS) for Technology B. In Figure 4 the
parameter s is set to zero whenever technology A captures more
than two-thirds (66.7%) of the market. Under these conditions, the system
always returns to competitive balance. This discussion is reflected in the decisions
that firms producing video game consoles and game software make regarding (backward)
compatibility of their products [70]. Once the dominant player in this field,
Sega effectively set its s to zero when it decided not to make its new
game console, the 32-bit Saturn, backward compatible to video games and
complementary products that the hugely successful 16-bit Genesis had relied on.
To challenge the subsequent dominant position of Sony’s Playstation, Microsoft enfranchised
Sega’s portfolio of successful video game titles as Sega had by then ceased to
produce consoles. Microsoft tried to tap into the network effects associated
with Sega’s portfolio of games and associated with the use of its operating
system [70, p.13] when it launched its Xbox game console.
|
Market share of techn. A
↑
50%
|

|
|
|
time →
|
|
Figure 4: If S agents no longer profit from the network
externalities for losing B technology (s = 0) lock-in to prevailing
technology (A) is broken [31, p. 317).
|
A government (competition authority) or dominant player can,
for example, demand from the Microsoft Company to publish the source code of
its operating system, allowing others to design their product such that they
will interface with it. A government may also actively provide information
about the Linux operating systems. For router software network effects of the
kind analyzed by Arthur may be weaker then for software that private
individuals buy and use since the actors acquiring it are more knowledgeable
and the software itself is compatible with more kinds of software at the
interfaces. Due to the way in which Linux is developed, however, there is
little incentive for producers to actively market Linux, and there is a low
likelihood that consumers will actually be knowledgeable about this complex product.
Government intervention, by providing information about open source software,
to prevent undue lock-in may then be warranted as it increases social welfare [71].
A government may for similar reasons consider mandatory adoption by public
agencies (ibid.). These scholars make their argument independent of the
question whether or not Linux is technically superior as the jury on this
matter is still out [see, e.g., 72]. These kinds of interventions may be
sufficient for a competitive balance to remain or be restored.
The market share of a technology which has lost the
competition can, paradoxically perhaps, not be improved in terms of current
competitive circumstances. As Yahoo did, giving away its browser after it had
lost the browser war with Microsoft’s Explorer [73], one may have to destroy
one’s own network effects and related competences thus changing the nature of
the competitive relations. Dissolution of the network effects may imply or
result in a radical innovation, as the technology is freed from those
contextual factors coupled with the development of the technology in the previous situation. Such a step down changes the selection environment for both technologies,
possibly freeing up space for re-entry into the market by the firm backing up
the previously locked-out technology.
In a corporate world, a shift of trajectory may require a
different set of corporate alliances [74] or, in anticipation of a possible
need to break-out, the development of a broader set of (technical) competences
than is actually required in extant market conditions [75]. Since the
technological restructuring is radical, it is based on a reconstruction and not
on existing practices. One may have to abstract from the current situation and
invoke a different knowledge base for making decisions. Firms that have distributed capabilities seem best equipped for this because the coordination problem is then
considered as a cognitive puzzle (ibid.). Analyzing such strategic policy
options for governments and firms in the light of the model of the lock-in of a
technology developed enables us to understand which policy may actually hope to
accomplish its objectives, and helps in devising additional, complementary
instruments. It also allows one to understand counter-intuitive effects of strategic choices.
A techno-economic system can increasingly develop along a
trajectory as two sub-systems interact at their respective interfaces. The
system may become locked-into a suboptimum because the fitness landscape may be
rugged [54, 55] as long as a third selection environment is relatively stable. The
reaction-diffusion dynamics enables us to understand how a lock-in between a
single technology and the market dynamics can be dissolved in a later stage. A
co-evolution along a single trajectory can be “unlocked” when the diffusion
mechanism of the market no longer co-evolves with the technical means of production.
When another selection environment becomes relevant to a previously locked-in system, the new configuration may begin to tilt the system as soon as
diffusion at the new interface becomes more important than, as suggested by Eq.
7, half of the rate along the trajectory of the system. Because an economic
production system is attracted by market opportunities, one can expect a trajectory
to be exploited to gain market share. The lock-in can thus be expected to erode
as the diffusion rate for the new technology increases. A third selection environment, for example of political or strategic decision making, can become relevant, and reaction-diffusion dynamics may then open the lock-in.
5. Conclusion
Lock-in may result from the co-evolution of two selection environments or sub-systems, such as between the economic and the technological environment. Break-out from a lock-in is possible, but has not been modeled so far in the
literature with a few exceptions [21]. This paper systematizes the discussion
about the circumstances for break-out from a lock-in by arguing that when a
third selection environment interacts with two locked-in ones, break-out or the
return to a competitive balance is possible [58, 76]. Introduction of the reaction-diffusion
mechanism into the model enables us to understand how such a process of
break-out can be analyzed as an endogenous outcome of the dynamics of a system.
It suggests conditions for the break-out of a lock-in or for return to a
competitive balance between two technologies. The model developed allows one to understand better what options agents have already been experimented with
actually do, and may suggest additional and possibly complementary ones, as
lock-in, break-out or a competitive balance between technologies is sought.
Acknowledgement
We are grateful to two anonymous referees and the editor for
comments and suggestions. The usual disclaimer holds, however.
return
References
[1] Arthur, W.
B., Competing technologies, in: Dosi, G., Freeman, C., Nelson, R., Silverberg, G., Soete, L., (Eds.), Technical Change and Economic Theory. Pinter, London, pp.
590-607, 1988.
[2] Arthur, W.
B., Competing technologies, increasing returns, and lock-in by historical events. Econ. J. 99(1989) 116-131.
[3] Carlsson, B.,
Internationalization of innovation systems: a survey of the literature. Res.
Pol. 35 (2006) 56-67.
[4] Carlsson, B.,
Stankiewicz, R., On the nature, function, and composition of Technological
systems, J. of Evol. Econ. 1 (1991) 93-118.
[5] Dosi, G.
Technological paradigms and technological trajectories, Res. Pol. 11(1982)
142-167.
[6] David, P.,
Technical Change, Innovation and Economic Growth. Cambridge University Press, Cambridge, UK1974..
[7] Rosenberg,
N., 1976. The direction of technological change: inducement mechanisms and
focusing devices, in: Perspectives on Technology. Cambridge University Press, Cambridge, pp. 108-125.
[8] Nelson, R. R.
and S.G. Winter, In search of useful theory of innovation, Res. Pol. 6 (1977)
35-76.
[9] Nelson, R. R.
and S.G. Winter, An Evolutionary Theory of Economic Change. Belknap Press of Harvard University Press, Cambridge, MA, 1982.
[10] Schumpeter,
J., Business Cycles: A Theoretical, Historical and Statistical Analysis of
Capitalist Process. McGraw-Hill, New York, [1939] 1964.
[11]
Malerba, F., R. Nelson, L. Orsenigo and S. Winter, Demand, innovation, and the dynamics of market structure: the role of experimental users and diverse preferences” J. of Evol. Econ. 17 (2007): 371-399.
[12]
Van den Ende, J. and W. Dolfsma, Technology-Push, Demand-Pull and the
Shaping of Technological Paradigms, J. of Evol. Econ. 15 (2005) 83-99.
[13] David, P. A., Clio and the economics of QWERTY. Amer. Econ. Rev. 75(1985) 332-337.
[14] David, P. A., 1999. At Last, a Remedy for Chronic QWERTY-skepticism! Unpublished manuscript,
Cargèse (Corse), France, 5-12 September 1999.
[15]
Liebowitz, S. J., Margolis, S. E., Winners, Losers & Microsoft:
Competition and Antitrust in High Technology. The Independent Institute, Oakland, CA, 1999.
[16] Cowan, R.
and S. Hulten, Escaping Lock-in: the case of the electronic vehicle, Technol
Forecast and Soc Change 53 (1996) 541-567.
[17] Grübler, A.,
Diffusion: Long patterns and discontinuities, Technol Forecast and Soc Change
39 (1991) 159-180.
[18] Islas, J.,
Getting round the lock-in in electricity generating systems: the example of the
gas turbine, Res Pol 26 (1997) 49-66.
[19] Leydesdorff,
L., Hyperincursion and the globalization of a knowledge-based economy, in:
Dubois, D.M. (Ed.), Proceedings of the 7th International Conference on
Computing Anticipatory Systems, CASYS’05. American Institute of Physics, Melville, NY, Vol. 839 (2006), pp. 560-569.
[20] Mowery, D.
C. and N. Rosenberg, N., The influence of market demand upon innovation: a
critical review of some empirical studies. Res. Pol. 8 (1979) 102-153.
[21]
Carrillo-Hermosilla, J. And G.C. Unruh, Technology Stability and Change: An
Integrated Evolutionary Approach, J. of Econ. Issues 40 (2006) 707-742.
[22] A. Kirman
and N. Vriend, Evolving market structure: an ACE model of price dispersion and
loyalty, J. of Econ. Dyn. and Control 25
(2001) 459–502.
[23]
Bikhchandani, S. D. Hirschleifer, and I. Welch, A theory of facds, fashion,
custom, and cultural change as informational cascades, J. of Pol. Econ.100
(1992) 992-1026.
[24] Adler,
M.,“Stardom and Talent, Amer. Econ. Rev. 75 (1985) 208-212.
[25] Pesendorfer, W., Design
Innovations and Fashion Cycles, Amer. Econ. Rev. 85 (1995) 771-792.
[26] Abernathy,
W. J., K.B. Clark, Innovation: mapping the winds of creative destruction. Res. Pol. 14 (1985) 3-22.
[27] Freeman, C.,
Perez, C., Structural crises of adjustment, business cycles and investment behaviour, in: Dosi, G., Freeman, C., Nelson, R., Silverberg, G., Soete, L. (Eds.),
Technical Change and Economic Theory. Pinter, London, pp. 38-66, 1988.
[28] Klepper, S.,
Industry life-cycles, Industrial and Corporate Change 6 (1997) 145-182.
[29] Kline, S.
and N. Rosenberg, An overview of innovation, in: R. Landau and N. Rosenberg (Eds.), The Positive Sum Strategy: Harnessing Technology for Economic Growth. National Academy Press, Washington, DC, pp. 275-306, 1986.
[30] Cusumano,
M.A., Y. Mylonadis and R.S. Rosenbloom, Strategic
Maneuvering and Mass-Market Dynamics: The Triumph of VHS over Beta,
Bus. History Rev. 66 (1992)
51-94.
[31] Leydesdorff,
L. and P. van den Besselaar, Competing technologies: lock-ins and lock-outs,
in: D. M. Dubois (Ed.), Computing Anticipatory Systems: CASYS'97. American
Institute of Physics, Woodbury, NY, Volume 437 (1998), pp. 309-323.
[32] Fisher, J.C.
and R.H. Pry, A simple substitution model of technological change. Technol.
Forecast. and Soc. Change, 3 (1971) 75-88.
[33] David, P. A.
and D.Foray, Dynamics of competitive technology diffusion through local network
structures: the case of EDI document standards, in: L. Leydesdorff and P.van
den Besselaar (Eds.), Evolutionary Economics and Chaos Theory. London: Pinter, London, pp. 63-78, 1994.
[34]
Bruckner, E., W. Ebeling, M.A.J. Montaño and A. Scharnhorst, Hyperselection
and innovation described by a stochastic model of technological evolution, in: L. Leydesdorff and P. van den Besselaar (Eds.), Evolutionary Economics and Chaos
Theory. Pinter, London. pp. 79-90, 1994.
[35] Leydesdorff,
L., Anticipatory systems and the processing of meaning: a simulation inspired
by Luhmann’s theory of social systems. J. of Artificial Societies and Social
Simulation, 8 (2005) Paper 7, at http://jasss.soc.surrey.ac.uk/8/2/7.html.
[36] Dubois, D.M., Computing
anticipatory systems with incursion and hyperincursion,
in: D.M. Dubois
(Ed.), Computing Anticipatory Systems, CASYS-First
International
Conference. American Institute of Physics, Woodbury, NY. Vol.
437, pp.3-29,
1998.
[37] May, R. M.,
Stability and Complexity in Model Ecosystems. Princeton University Press, Princeton, NJ, 1973.
[38] Sonis, M.,
Innovation diffusion, Schumpeterian competition and dynamic choice: A new
synthesis. J. of Sci. and Industrial Res. 51 (1992) 172-186.
[39] Sonis, M.,
Nonlinear socio-ecological dynamics and first principles of collective choice
behavior of “homo socialis”. Progress of Theoretical Physics, 139 (2000)
257-269.
[40] Nijkamp, P.
and A Reggiani, Evolutionary dynamics in technological systems: a multi-layer
niche approach, in: L. Leydesdorff and P. van den Besselaar, P. (Eds.),
Evolutionary Economics and Chaos Theory. Pinter, London, pp. 93-108, 1994.
[41] Sahal, D.,
Technological guideposts and innovation avenues, Res. Pol. 14 (1985) 61-82.
[42] Waddington, C. H., The Strategy of Genes. Allen &
Unwin, London, 1957.
[43] Leydesdorff,
L. and P. van den Besselaar, Technological development and factor substitution
in a non-linear model. J. of Soc. and Evol. Systems 21 (1998)
173-92.
[44] Geels, F.W.,
The hygienic transition from cesspools to sewer systems (1840-1930) : the
dynamics of regime transformation, Res. Pol. 35 (2006) 1069-82,
[45] Arrow, K.
J., The economic implications of learning by doing. Rev. of Econ. Stud. 29
(1962) 155-173.
[46] Sahal, D.,
Alternative conceptions of technology. Res. Pol. 10 (1981) 2-24.
[47] Andersen, E.
S., Evolutionary Economics: Post-Schumpeterian Contributions. Pinter, London, 1994.
[48] Abernathy,
W.J. and J.M. Utterback, Patterns of Innovation in Industry, Technol. Rev. 80 (1978) 40-47.
[49] Anderson, P.
and M.L. Tushman, Technological discontinuities and dominant designs: a
cyclical model of technological change, Admin. Sci. Quart. 35 (1990) 604-633.
[50] Nelson, R.
R., Economic growth via the coevolution of technology and institutions, in: L.
Leydesdorff and P. van den Besselaar (Eds.), Evolutionary Economic and Chaos
Theory,. Pinter, London/ New York, pp. 21-32, 1994.
[51]
Poincaré, H.,. Lecons de mécanique céleste.
Gauthier-Villars, Paris, Vol. 1905 vol. I, 1907 vol. II part I, 1909
vol. II part II, 1911 vol. III.
[52] Li, T.-Y.,
Yorke, J. A., Period three implies chaos, Amer. Mathematical Monthly, 82 (1975)
985-992.
[53] May, R. M.,
Leonard, W. J., Nonlinear aspects of competition between three species. SIAM J. of Applied Mathematics 29(1975) 243-253.
[54] Kauffman, S.
A., The Origins of Order: Self-Organization and Selection in Evolution. Oxford University Press, New York, 1993.
[55] Frenken, K.,
A complexity approach to innovation networks. The case of the aircraft industry
(1909-1997), Res. Pol. 29 (2000) 257-272.
[56] Leydesdorff,
L., The complex dynamics of technological innovation: a comparison of models
using cellular automata, Systems Res. and Behavioural Sci. 19 (2002) 563-575.
[57] Levinthal,
D. The slow pace of rapid technological change: gradualism and punctuation in
technological change, Industrial and Corporate Change 7 (1998) 217–47.
[58] Leydesdorff,
L. The Knowledge-Based Economy: Modeled, Measured, Simulated. Boca
Raton, FL: Universal
Publishers, 2006b.
[59] Rashevsky,
N., An approach to the mathematical biophysics of biological self-regulation
and of cell polarity, Bull. of Mathematical Biophysics 1 (1940) 15-25.
[60] Turing, A.
M., The chemical basis of morphogenesis. Philosophical Transactions of the
Royal Society, Series B, 237 (1952) 37-72.
[61] Rosen, R.,
Anticipatory Systems: Philosophical, mathematical and methodological
foundations. Pergamon Press, Oxford, etc., 1985.
[62] Dolfsma,
W. (2009) Institutions, Communication and Values.
Houndsmills:
Palgrave
Macmillan.
[63] Leydesdorff,
L., Configurational Information as Potentially Negative Entropy: The Triple
Helix Model. Entropy 10 (2008) 391-410; available at http://www.mdpi.com/1099-4300/1010/1094/1391.
[64] Metcalfe,
S., Evolutionary Economics and Technology Policy, Econ. J. 104 (1994) 931-944.
[65] Edlin, A. and S. Reichelstein (1996) "Holdups, Standard
Breach Remedies, and Optimal Investment" Amer. Econ. Rev. 86(3): 478-501.
[66] Anand, N. and R. Peterson, When
market information constitutes fields:
Sensemaking of markets in the commercial music
field, Organ. Sci. 11 (2000)
270-84..
[67] Collingridge,
D., The Social Control of Technology. The Open University, London, 1980.
[68] Frenken, K.
and L. Leydesdorff, Scaling trajectories in civil aircraft (1913-1970). Res.
Pol. 29 (2000) 331-348.
[69] Leydesdorff,
L., Technology and culture: the dissemination and the potential ‘lock-in’ of
new technologies. J. of Artificial Societies and Social Simul. 4 (2001), Paper
5, at <http://jasss.soc.surrey.ac.uk/4/3/5.html>.
[70] Schilling,
M.A., Technological leapfrogging: Lessons from the U.S. videogame industry,
California Man. Rev. 45 (2003) 6-32.
[71] Comino, S.,
F.M. Manenti, Government Policies Supporting Open Source Software for the Mass
Market, Rev. of Industrial Organ. 26 (2005) 217-240.
[72] Schmidt, K.M., M. Schnitzer, “Public Subsidies for Open
Source? Some Economic
Policy Issues of the Software Market” Harvard J.
of Law & Technol. 16 (2003)
473-
[73] Windrum, P., Leveraging technological externalities in complex technologies:
Microsoft’s exploitation of standards in the browser wars. Res. Pol.
33 (2004)
385–394.
[74] Dittrich, K., G. Duysters,
and A.P. de Man, Strategic repositioning by means of
alliance
networks: The case of IBM. Res. Pol. 36(2007) 1496-1511.
[75] Granstrand, O., P. Patel and K. Pavitt,
Multi-Technology Corporations: Why they
Have ‘distributed’ rather than
‘distinctive core’ competences, California
Man. Rev.
39 (1997) 8-25.
[76] Etzkowitz, H. and L. Leydesdorff, The Dynamics of Innovation: From
National Systems and ‘Mode 2’ to a Triple Helix of
University-Industry-Government Relations. Res. Pol. 29 (2000) 109-123.
return




