return

Sustainable Technological Developments

and Second-order Cybernetics

 

Loet Leydesdorff

Science & Technology Dynamics, University of Amsterdam

 

Technology Analysis & Strategic Management 9(3) (1997) 329-341

 

            Abstract

 

                        Using second-order systems theory, the concept of “sustainability” shifts from a normative starting-point to a probabilistic expectation that is open to investigation.  While first-order systems can be considered as observable translations of input into output, second-order systems theory adds the perspective of evolution to networks of first-order systems.  Complex and dynamic systems are not instructed by incoming signals, but disturbed.  They are able to adapt the cycles of their behaviour.  Consequently, second-order delineations are not “given,” but continuously reconstructed.  These systems have no “natural” delineations, and their “limits to growth” remain a provisional hypothesis.  The likelihood of the various progressions can be specified only in terms of a model.  Among other things, changes between technological trajectories within the current regime can be distinguished from the possible transition to a regime of sustainable technological developments.

 

 

Introduction

 

            The “sustainability” of a development was put on the research agenda of systems dynamics from the side of the engineering sciences.  For example, the control of output flows in chemical industry is an issue for engineering.  The simulation of a system of fluxes using computers is a typical extension of this problem formulation.  The (first-order) flow model can be generalized to social problems like population or pollution control.[1]  Social systems, however, are complex dynamic systems.  Like individuals, social systems may adapt to changes in their environments using mechanisms which cannot be described fully in terms of input- and output-flows: adaptation and learning are reflexive mechanisms.

            In a first-order systems model, relations are specified on the basis of assumptions that do not change during the simulation.  Levels, sinks, and sources are not further analyzed in terms of their internal behaviour.  For example, income distribution is averaged when an indicator for income development (e.g., GNP per capita) is declared, while a potentially autonomous effect of the form of income distribution on further developments is usually ignored.  In second-order systems theory, the potential effects of the recursive behaviour of (sub-)systems in response to external disturbances is made central to the analysis.

            Figure One illustrates the Gestaltswitch:[2] the recursive view of the system takes a perspective which is perpendicular to the behavioural one.  While first-order systems theory focuses on input-/output-flows in terms of behaviour of systems (acknowledging for feedbacks), second-order cybernetics studies the evolution of systems which exhibit recursive developments.

 

 

 

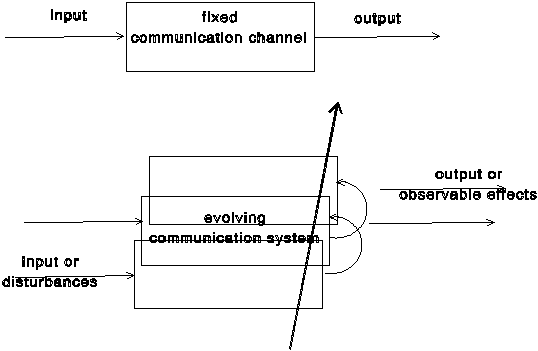
1Figure 1

A communication channel which transforms input into output, versus an evolving communication system

 

            For social systems, the metaphor of an evolving system is more adequate than the behavioural perspective.  From the latter perspective, systems theory may lead to the reification of social categories.  Actors or groups of actors, however, are able to change their behaviour reflexively.[3]  From the recursive perspective, the social system can be considered as a complex and evolving network of communications which is added to the actors who carry it at the nodes.[4]  The recursive operation of the network upon itself is the interactive result of actions taken at the nodes.  Since this communication system is not expected to be in equilibrium, changes in behaviour at the nodes can have unexpected effects on the further development of the network system.

            While first-order systems theoreticians have pointed to the potentially counter-intuitive response of social systems to policy interventions,[5] second-order systems theory adds another layer of complexity.  Among other things, second-order systems theory is able to explain why first-order models fail in their prediction of global crises on the basis of the “World”-models of Meadows, Forrester, and the Club of Rome.^1,5  These earlier models adopted a behavioural perspective to the problems by specifying input/output relations among sub-systems; second-order cybernetics assumes that a complex dynamic system which is not in equilibrium cannot be “fixed” in terms of its operations.

 

The surplus-value of first-order systems theory

 

            The numerical approach-using the computer-enables us to study systems of differential (or difference) equations which are mathematically too complex for a generalized solution.  The algorithmic simulation model allows us to search the parameter space for combinations and optimizations other than the ones which occurred historically.  But the historical events allowed us initially to specify these relations.  As everybody who has tinkered with first-order models knows, the further development of the model requires the analyst to modify the initial specifications into more sophisticated ones.  This process of reformulation itself has theoretical value, since by tinkering with the model one improves one’s understanding of the assumptions which went into the construction of the model.[6]

            Additionally, first-order systems theoretical models enable us to demonstrate interaction effects (e.g., “synergism”).  While the effects of a certain development can only partially be understood by focusing on this development from each theoretical perspective, the partiality of the various perspectives can be combined systematically into a model as a set of (e.g., differential) equations.  For example, the large-scale planning models which allow for the prediction of national economic growth rates, etc., are based on the exploitation of the algorithmic approach over discursive explanations.  Paradigmatic discourses provide us with “situated” windows on the complex and dynamic systems under study.  The paradigms are expected to be “incommensurable”[7] when the windows are nearly orthogonal.[8]  A first set of counter-intuitive relations can be revealed when the geometrical metaphors are combined using algorithmic simulations.

            These potentially counter-intuitive results of first-order systems models enable the reflexive methodologist to raise the following question: when do the interactive effects necessitate the respecification of the initial assumptions?  This problem can be formulated in two ways: with reference to the a priori specifications and/or with reference to the a posteriori state of the model system.  Do the counter-intuitive results indicate that the ex ante specifications should be revised or do they indicate that an emerging category should be declared?  Note that the emerging category cannot be specified without running the simulation.  Therefore, it is a dynamic effect of the model (i.e., ex post), while the respecification of the model on the basis of improved understanding remains logically ex ante.

            Does this analytical distinction have practical value?  In my opinion, it provides us with insight into the relations between theoretical specifications and algorithmic modelling with particular relevance to the theme of this paper.  For example, if one were able to bring a social system into a state which is environmentally friendly and sustainable-like an option in the Meadows-models-would such an emerging state of the system differ so much from its present state that various relations would have to be respecified?  In general, if the system achieves a desirable state of affairs, would the qualitative transition ipso facto require the reconsideration of the categories and relations which spanned the model system, thus potentially invalidating the initial prediction?

            A first-order model is time-stamped at the moment of the model specification, and thus by definition it cannot predict what will happen if the system under study achieves a qualitatively different stage.  But one can assess the system’s state at each moment in time, for example by using multi-variate analysis to reveal the latent structure of the system.  Changes at the structural level can be studied with hindsight.  Thus, the analyst seems caught in a methodological dilemma: either one studies the multi-variate changes in the network ex post, or one predicts ex ante by making assumptions about the endurance of assumed relations.  This introduction of the time perspective as a problem brings us more definitively into the realm of second-order systems dynamics.[9]

 

 

Second-order systems dynamics

 

            The remaining cosmological assumption in first-order systems theory has been the idea of a single system’s clock.  One has to assume such a clock in order to predict in 1970 that a world crisis will occur in 1990 or to predict in 1990 that such a crisis will occur before 2030.[10]  Second-order systems theory assumes that all recursive systems and sub-systems tick with their own frequencies, and that synchronization requires explanation.[11] For example, the biological clocks of human beings are expected to perform a circadian cycle of approximately 25 hours.  Our daily routines are updated by the social system which assumes a synchronization at each 24 hours.[12]  However, note the cultural character of these daily cycles of 24 hours, since the days are shorter in winter than during the summer.  One conventionally accepts, for example, “daylight saving time”: historical time can be considered as a function of social relations with an external reference to an assumed “physical time”.[13]

            The issue of “time” is pertinent to our problem for various reasons.  Modernization, first, increases the speed of social developments.  While previous civilizations managed to maintain specific orders for millennia, global disorders like the hole in the ozone layer and the greenhouse effects seem the results of a single century of industrialization.  Furthermore, social processes in a pluriform and differentiated society are expected to develop with different speeds.  Second, the time axis is urgent in relation to solutions.  Beck,[14] for example, argued that previous generations could “wait and see” to the impacts of their actions, while currently one has to anticipate risks which one cannot even see or smell.  The risks remain expectations on the basis of scientific theories.  Is one able to protect oneself against hypothetical and yet potentially global risks?  Third, the whole idea of “sustainability” introduces time into the representation of “future generations” whose assumed interests should be offset against the tendency in an evolutionary system to continue its regime despite potentially immanent crises.  In a second-order systems model synchronization and harmony have to be explained.

            Recursive systems operate with one or more internal ticks.  As noted, a first-order system can be described as a black box which transforms input into output like a mirror or a fixed communication channel; a second-order system has an evolutionary axis perpendicular to the transformation of input into output.  From a recursive perspective, the system is not instructed by the input (for producing an output), but only disturbed.  In adapting to the disturbance according to its own regime, it may exhibit an output.[15]  Thus, the recursive view is contextual, and consequently, it tends to be “incommensurable” with an analysis in terms of input and output, or in terms of external causes and effects.  The second-order communication system is operationally closed: it communicates what it communicates, and the observer has access to its substance only in terms of representations using his/her own system of communication (e.g., “discourse”).

            The first-order representation of sub-systems hanging together in a network derives from a behavioural view, but the development of the network itself is considered recursively during the computer simulation by declaring a clock.  From a second-order perspective, the (sub‑)systems composing the network are themselves also developing networks.  The next-higher level is composed of (unintended) interactions among the lower-level exhibitions of output.  But as noted, the analyst turns ninety degrees at each step from a behavioural into a recursive perspective, and the representations are therefore expected to be incommensurate.  Thus, the relation between networks at different levels should not be considered as a multi-level problem of aggregation; the evolutionary achievement of a next-higher level can be decided only on the basis of the interaction terms (as opposed to hierarchical aggregation).  The higher level is expected to have an orthogonal function for the lower level, and vice versa.

            For example, if human beings interact using language or other means of social communication, the social system can be seen as the product of their interactions.  Each interaction can have a different meaning for each of the interacting agents.  The codification of the interaction in terms of symbolic meaning, and thus perhaps social structure, is a function of the network which can no longer be attributed solely to specific interactants.  Of course, this symbolic meaning can be given a meaning by each of the reflexive interactants.  Meaning is discretionary to the recursive system; for example, it can be changed reflexively (e.g. on psychological grounds) by the individual actor.  These psychological concerns, however, are of a completely different origin from the sociological ones (although each interactant may try to impose his or her definition on the situation).  The social networks and the symbolic meanings (or codifications) entailed in them have their own dynamic; these systems operate in terms of interactions among the carrying systems, and thus the substance of their communication is expected to be different.

            As noted, second-order systems can be considered as recursive operations on distributions of first-order systems.  When the lower-order systems are observed, the distributions remain constructions.  From a network perspective, the lower-level systems (“actants”) translate input into output.[16]  The dynamics of the higher-order network add a clock to the network.  But at each lower level, each of the sub-systems contain clocks with their own routines and update frequencies.  All these “self-organizing” systems operate in their present by reorganizing the possible representations of their pasts in relation to incoming disturbances.

 

 

Is one able to forecast on the basis of second-order systems theory?

 

            How do systems develop which are no longer defined in terms of observable instances, but in terms of distributions and networks among observables?  If the future is no longer expected to remain the same as the observable past, what then are the dynamics which enable us to specify an expectation with reference to complex systems?  Evolutionary and non-linear perspectives have provided us during recent years with the possibility of answering these questions.

            Dissipative structures are not in equilibrium, and consequently, they tend to dissipate energy until they reach equilibrium.  All systems drift; but the drift is constrained by the structural characteristics of the system.  The constraints generate “friction” during the interactions, and on the basis of the disturbance terms non-linear systems of probabilistic entropy emerge.[17]

            If the sub-systems are orthogonal dimensions of the super-system with their own routines, how then can one analyze this self-organization?  The interactions among lower-level systems continuously disturb developments at the higher level.  These disturbances if repeated over time, may exhibit systemness.  Thus, all interaction terms have to be declared and examined on the emergence of systemness.  In other words, the phase space is equivalent to the saturated model that contains all the interaction terms.  Theoretical specifications restrict the number of possible interactions, and thereby the system becomes “computable.”  Additionally, all loops may intersect.  Note that this was formally forbidden in traditional computer languages, because then different options for further developments are possible.  In other words, the system would no longer be “fixable” in terms of its parameters: two different runs with similar parameters might lead to different results for stochastic reasons if the various loops are allowed to disturb one another.

            The model of parallel and distributed processing provides us with a metaphor to understand the intersecting routines.  Both the processors and the server at the network level run their own routines.  Messages are sent which may disturb procedures at other places.  In an open network structure these disturbances are stochastic from each local perspective.  Thus, the order is not fixed ex ante as a (potentially counter-intuitive) consequence of the theoretical specifications, but emerges ex post as an interactive and unintended result.  Order is not given originally, but reconstructed at the receiving end.

            Does this mean that we have to give up all hope of prediction?  In my opinion, it does not.  As noted, first-order simulations enable us to improve on first-order theories.  First-order theories aim at stabilizing a representation in the discourse: they aim at improving a geometrical metaphor by taking a perspective on the subject of study.  A discursive stabilization remains provisional, but sometimes one is able to add reflexively to one’s scientific discourse the question of how long one expects the hypotheses to continue to be confirmed.  In other words, one is able to specify the system(s) of reference in the time dimension.[18]  While the basic laws of physics may hold for long distances and long time stretches, evolving systems are expected to go through irreversible transitions after which not only their operation but even their “nature” may have changed.  Thus, new categorical terms may be needed for the description.  For example, a theory which provides us with correct predictions in the case of an undifferentiated early embryo may no longer hold true for a fully differentiated biological system.  Analogously, a dinosaur is not expected to exhibit dinosaur-like behaviour when introduced into Jurassic Park!

            Our only access to limiting the number of possible combinations, however, is by theorizing about the events that have occurred.  Events can be considered as the outcomes of interactions that have (provisionally) been stabilized.  For example, a human body seems to be sustainable for approximately hundred years.  Theoretical descriptions of these events inform us about the structural constraints which we expect to act as selective operators on the complexity.  Without theories we would be lost, but second-order cybernetics is reflexive about the contextual nature of theorizing.  At an epistemological level, this reflexivity makes us aware that our theoretical insights are contingent and historical: our provisional hypotheses have a different status than Karl Popper’s truths which transcend to World Three.[19]  Among other things, this reflexive status allows us to entertain rather unlikely and bold theories.  Theories can be more or less codified, but their epistemological status remains hypothetical.

            Can these evolutionary insights be falsified?  What might count as instances which could be used for measurement?  The primary question susceptible to measurement is the hypothetical delineation of the system and its sub-systems.  Which networks (or more generally, distributions) shall we consider as systems, and how is each system’s level composed of sub-systems?  The hypothesis of a system can be tested by measurement since system components are expected to develop in relation to one another (e.g., to exhibit the Markov property), while non-systems are expected to develop in uncorrelated fashion.  Using probabilistic entropy measures from information theory, one is able to analyze whether the observed interactions in the substantively hypothesized domains are organized in terms of structures, and whether or not patterns are maintained.[20]

            In general, the expectation for an evolutionarily complex system is that it will develop functionally differentiated sub-systems which operate with frequencies an order of magnitude higher than the higher-level system.  The higher-level system is a network of “weak links” on top of more densely packed lower-level systems.[21]  In the longer run, functional differentiation is expected since each system may be “locked into” a specific (co-evolving) environment for stochastic reasons.[22]  Functional “resonances” between systems and environments selectively filter noise.  While complex systems are by definition composed and thus differentiated, functional differentiation is a specific arrangement with reference to a higher-order of systems development.  As noted, this order is emergent.  When one system has become functional for the higher-level development, the resonance is expected to entrain other parts of the system into functionality.  However, the super-system may go through a next transition before this lower-level adjustment has fully taken place.

            In summary, we are able to specify expectations and to indicate measurement instruments for second-order simulations.  Of course, our indications are rather crude, and the elaboration into standard software packages like those presently available for first-order systems theory (e.g., DYNAMO; STELLA),[23] still requires considerable development.  Above, we have mainly tried to provide the reader with a window on the potentials of second-order cybernetics for reformulating crucial theoretical questions of first-order cybernetics.  We now turn to some important consequences of the new cybernetics for “sustainable developments.”

 

 

Consequences for “Sustainable (Technology) Developments”

 

a. system/environment distinctions

 

            The most important consequence of second-order systems theory, in my opinion, is implied in considering the system/environment distinction no longer as a given, but as potentially dynamic.  Thus, the system remains a hypothesis and should never be reified.  The second-order system is an expectation with respect to the (development of the) distribution of lower-level systems.  Over time, its relation to the environment may have to be reconsidered.  Redefinitions may have implications for the definition of lower-level constructions since knowledge is based on constructions “all the way down”.

            Obviously, this reformulation of the system/environment distinction has consequences for “environmental” studies.  Neither the systems nor the environments are given.  In second-order systems theory, it makes little sense to speculate about performance indicators of “environmental utilization spaces”[24] without further reflection about the hypothetical delineation of such spaces.  Not even “the global system” should be considered as a given, since it matters how a system is organized.  Any “given” or “natural” delineation can be considered as provisional using second-order systems theory.  Correspondingly, the urgency of any problem has to be specified in relation to a contingent time axis.

            For example, in the context of the discussion of “limits to growth,” one may wish to raise the question of whether there is a maximum capacity of North-South transport across the Alps?  Does the notion of sustainable development imply that one should distribute the total capacity for transportation across the Alps among the various nations of Northern and Southern Europe, as previously one had to allocate fish quota in the North Sea?  From the perspective of second-order cybernetics, any determination of a maximum capacity for transport across the Alps remains a hypothesis that takes the present state as the system of reference.  First, one may wish to build more tunnels under the Alps so that a larger number of trains can be added to the current means of transportation.[25]  But beyond that, our imagination of future means of transport across the Alps is limited by our present mindset.  Nobody could imagine a century ago that we would have, in addition to roads and railroads, corridors for transporting large numbers of people and goods over the Alps by air.

            What we wish to demonstrate with this example is that structural elements that are added to the network of roads, e.g. as a differentiation, add new dimensions to the problem of determining the maximum capacity of a system.  In general, while a dissipative system tends to become overburdened by the fluxes that it creates, the interactions may trigger further differentiation, and thereby extend the system into other dimensions.  As will be shown below, each added dimension is a multiplier of previously existing possibilities.  From this perspective, the system can grow exponentially by improving its internal organization.  (But the reproduction of the system may become increasingly burdened with further differentiation.  I return to this issue in a later section.)

            One is inclined to use biological metaphors in assessing the problem of environmental pollution as a problem for the social system.  However, the biological metaphor is fundamentally mistaken.  All biological systems tend to die.  In our culture, a psychological identity is thought to die with the biological body.  But society should not be considered as a living system in the biological sense: it is the network of communications between us, with its patterns of institutionalization.  It has no “natural” limits as long as there are actors to perpetuate it.  Social systems can be reorganized: tunnels are added to the Alps, the maximum capacity of transportation increases.  If one would breed herring in the North Sea, one might be able to increase the fish quota.  The question is whether a cycle with another frequency can be added to and maintained by the system(s) under study.

            Let us further clarify the issue by the following formalization: a network can be represented as a matrix or a two-dimensional probability distribution (n x m).  Thus, its capacity is determined boht by the number of units (n) and by the number of communications among these nodes (m).  As long as m is low, the number of units can be used as an indicator of the capacity of the system.  But with each increase of m, the influence of the number of units decreases.  For example, the population density is not so important for the pollution of large cities as the quality of the sewage system, i.e., the complexity with which this system is infrastructurally organized.  What matters is the complexity of the pattern of differentiations.  The modern social system seems only sustainable on the condition that it be continuously differentiated, and thus subject to innovation.

            Of course, these ideas have been articulated before in discussions of environmental policies.  Second-order systems theory, however, provides these positions with legitimation: the evocation of “natural” constraints is one discourse among other possible discourses, and it is doubtful whether it is a particularly fruitful discourse since it is based on a biological metaphor for studying social problems.  Second-order systems dynamics provides us with metaphors which are more sophisticated than the first-order ones, both in terms of their explanatory power and their power to guide us in the search for alternative solutions.

 

b. sustainability

 

            The methodological gist of second-order cybernetics lies in making our concepts themselves reflexive and dynamic by declaring them as hypothetical, i.e. constructions in constant need of an update.  The external referents are no longer considered as “givens,” but represented as assumptions in reflexive discourses that themselves may be changed in a subsequent update.  How does this reflexivity of the discourse affect the prevailing notion of “sustainability?”

            Remember the definition of sustainability in Brundtland’s (1987) report about Our Common Future (at p. 9):[26]

 

            Yet in the end, sustainable development is not a fixed state of harmony, but rather a process of change in which the exploitation of resources, the direction of investments, the orientation of technological development, and institutional change are made consistent with future as well as present needs.

 

This definition provides us with a dynamic perspective on lasting harmony.  Second-order systems theory, however, provides us with arguments to define “sustainability” with reference to defined periods of time.  In a contingent world, nothing can be sustained for ever; crisis is ever pending in a dissipative structure.  The crucial question is: What is the time-axis of each development?  For how long does one want to develop a specific system? 

            Perhaps second-order cybernetics has its most fruitful applications in reflections about the time axis.  Harmony can be considered as potential resonances among different frequencies.[27]  Emerging resonances among the various cycles of communication may provide us with new opportunities.  For example, a tendency has been noted to form networks in advanced industrial countries among representatives of industry, government, and scientific institutions.  Such networks are able to elaborate research programs which none of the parties can support during the envisaged time period without the help of the other parties.[28]

            In the Rotterdam harbour, for example, a network-activated by state representatives- achieved the use of left-over hydrogen from petrochemical plants for transport needs felt at other places and by other industries in the same area.[29]  None of the individual firms could overcome the thresholds for the investments, nor without this intervention would they even have imagined putting the problem on the agenda for a subsidy.  If one is able to reorganize communications with different frequencies into new network arrangements, considerable profits can be expected in due time.

            While such an arrangement can be considered as an important example of “sustainable technological development,” it is expected to provide a solution in terms of decades, and not in terms of centuries.  In summary, the sustainability of a development has to be related to the sustainability of the envisaged solution for a specific time period, and not with reference to “sustainability” at a global level.  We turn now to the relation between local and global solutions.

 

c. trajectories and regimes

 

            One fundamental lesson taught by second-order cybernetics is the following: one can imagine trajectories in terms of geometrical representations,[30] while regimes are next-order distributions of possible trajectories.  Thus, a trajectory is a sub-dynamic of a regime.[31]  But the regime cannot come into being otherwise than via a trajectory.  The trajectory comes first, the regime remains emergent.  The trajectory is observable, and thus measurable, while the regime remains a hypothesis.

            The geometrical representation requires three dimensions; but the regime is additionally complex with a fourth degree of freedom: it is contingent in time and space.  Therefore, one has to study it both in terms of its visible behaviour, i.e., in terms of its instantiations,[32] and in terms of assumed fluxes in structural parameters.  However, such concurrent change at both levels overloads our linguistic capacities: using “natural” languages we are able to communicate in order “to draw the picture,” but for the representation of a regime one needs a movie in which both the data and the perspective from which one assesses the data may change.  The replacement of the variable language with the conceptualization in terms of fluxes (dx/dt) allows for changes both in terms of the value of a variable, and in terms of the meaning of a category.  This can be made visible by “animating the simulation.”

            The algorithmic simulation allows us to envisage possibilities which are counter-intuitive in discursive representations, and yet to control in terms of the underlying computer code whether one communicates only about phantasies and daydreams (p 6 0) or about possible options in the system (p > 0).  The likelihood of the events can be made the subject of study, since the events which are observable in the animation, can be backtracked to the underlying computer code.  The computer language codifies the discursive insights that went into the construction of the model.

            Note the relation between discursive specification and algorithmic modelling.  On the one hand, the scientific discourses can be considered as the “genotypical” specifications of the “phenotypes” which can be made visible on the screen.[33]  Only lower-order dynamics can be made the subject of theorizing because of the need to choose a perspective.  On the other hand, appreciation of the simulation results challenges the discursive theories, since these results are based on none of the used theories in isolation.  From this perspective, the phenotypical result is yet another sub-dynamic which may require another metaphor for the understanding.

            “Sustainable technologies” that implicate a transition at the level of a regime are expected to be counter-intuitive solutions from the perspective of a “natural” or (first-order) “theoretical” understanding.  As a normative implication, the assessment of whether a given development is organized into a regime or occurs only as a trajectory has important consequences.  For example, the car system can be considered as a regime with its own order.  Taxing leaded petrol may lead to different car engines but not to a replacement of cars by other means of transportation.  Since a regime is expected to contain a strong mechanism of adaptation, one expects no success in influencing the regime by direct policy actions.  But one can influence the trajectories belonging to a regime as sub-dynamics.  For example, one can enforce the implementation of a clean engine (or a noiseless engine in the case of airplanes).

            The choice between regimes remains in the domain of counter-intuitive expectations.  Second-order models may help to sensitize us to problems of regime change, but the result may be an early awareness rather than an option for deliberate change.  However, early awareness can help us to profit fully from emerging technological options, since the emerging perspective may still be optimizable on “sustainability” if the time scale can be specified.

 

d. sub-optima, hill-climbing, and/or change of regimes

 

            The algorithmic approach enables us to envisage the problem space spanned by the theoretical insights about aspects of the problem(s) under study.  Each partial perspective adds equations to the model.  As noted, in second-order cybernetics one considers these equations as representations of the structural constraints on the complexity.[34]  Interactions among structural constraints are expected to create local trajectories of possible solutions.  Since the system tends to be differentiated (see above), the trajectories are expected to be separated by overwhelmingly empty spaces.

            A solution is an optimization in the problem space.  The situation which historically occurred is considered only one among other possible sub-optima.  It is a viable option, since it did occur.  The “physis” of a system (its generation and reproduction) is one of its sub-dynamics.  Other important sub-dynamics include the “value” of a system in relation to possible alternative solutions at a particular moment in time (e.g., on the market); the specific co-evolution of a system with its environment;[35] and the “survival value” of this arrangement from an evolutionary perspective (i.e. using a time axis).

            The crucial point is that an existing system is by definition a local sub-optimum in a multi-dimensional space of possible solutions.  At other places in this space there may be other solutions which are by definition differently optimized.  The transition from one region in the phase space to another may be extremely difficult, since it can be associated with a change in regime.  The question can also be raised whether there exists a pathway from one part of the phase space to another.[36]  The common metaphor is one of hill-climbing: if one sits on one hill, further improvement may mean going up hill, although a change of hills may in the long term be more advantageous.[37]  In my opinion, one is in urgent need of computer models that capture these dynamics for problems of environmental concern and technological innovation.[38]

            One question crucial for the application of systems theory to environmental concerns originates from the expectation of global crises.  On the one hand, a functionally differentiated system should be able to process more complexity with increasing differentiation.  On the other hand, by enhancing differentiation the system drives itself towards a crisis: the interactions between the sub-systems tend to become decreasingly frequent with increase in functional differentiation, and thus the system is at risk of falling apart.  This phenomenon has been called “self-organized criticality”; it can be measured in terms of 1/f noise.[39]  Once the system has become critical, one may be inclined to take higher risks to change it.  As noted, radical change may have the character of a catastrophe, and therefore the effects may be rather unpredictable.[40]

            For example, several authors have pointed to the internal weaknesses of the communist systems in the former Soviet Union and in China before the end of the Cold War.[41]  At the end of the 1980s these systems seemed to have survived themselves; acute situations of crisis arose in 1989.  While the chances for improvement through transition seemed better for Russia than for China, at this moment China seems to have succeeded in finding a trajectory towards the regime of the Newly Industrializing Countries in the Pacific Region, while one could argue that Russia has failed to find its way to a capitalist regime.  Thus, in addition to the possibility of spotting a local sub-optimum in the nearby environment, the question has to be raised of the flexibility of the pathway towards the desired arrangement.

 

 

Conclusions

 

            With reference to the high hopes formulated in the Brundtland Report, it seems useful to emphasize that apart from its political realizability, the possibility of a transition towards “sustainable development” remains a theoretical hypothesis.  However, even if the likelihood of a transition is extremely low in the model, “tunneling effects” have been signaled.  “Niche management” seems particularly important in generating innovations which are otherwise unlikely.[42]  The additional dimension of “management” increases the organizational complexity of the system under study.

            In my opinion, the major advantage of second-order systems theory for the study of environmental concerns is the shift of focus away from “given” environmental constraints that are sometimes said to instruct us in taking action, and towards more attention for the hypothesized operations of the networks under study.  These networks are not “fixed,” but have to be delineated with reference to the assumed operations.  Action at the nodes can then be considered as variation; the network selects.  Some selections are selected for provisional stabilization.  Provisionally stabilized trajectories can be globalized into regimes, but a regime can only be studied if an emerging selection is hypothesized.  More complex systems are expected to be more easily sustainable than less complex ones, since the potential “resonance” among various sub-dynamics can provisionally buffer a complex system against disturbances.

            The Gestaltswitch from the behavioural perspective to the recursive perspective corresponds to a paradigm switch between first-order and second-order systems theory, indeed.  Previous arguments of social scientists against first-order systems theory do no longer apply to second-order systems theory.  For example, second-order systems cannot be reified while they remain by definition an expectation.  Additionally, second-order systems theory is able to provide us with a host of theoretical and empirical questions, both in the time dimension and in relation to the complexity of scientific representations.  The concepts of “limits to growth” and “sustainability” can be reformulated as empirical hypotheses-as opposed to the normative constraints that are often imposed on models using only a first-order understanding.

 

return

 

Notes and References