Meaning, Anticipation, and Codification in Functionally Differentiated Systems of Communication

return

Meaning, Anticipation, and Codification in

Functionally Differentiated Systems of Communication

Loet Leydesdorff

Science & Technology Dynamics, University of Amsterdam

Amsterdam School of Communications Research (ASCoR)

Kloveniersburgwal 48, 1012 CX Amsterdam, The Netherlands

loet@leydesdorff.net ; http://www.leydesdorff.net

In: Thomas Kron, Uwe Schimank, and Lars Winter (Eds.),

Luhmann simulated –

Computer Simulations to the Theory of Social Systems

1. Introduction

In order to generate and process meaning, a communication system has to entertain a model of itself. A system which contains a model of itself can function in an anticipatory mode. The anticipatory subsystem operates on the system from the perspective of hindsight, and thus an observer can be generated. The hindsight perspective is based on advancing the clock of the modeling subsystem by one time-step. From this next stage the model looks back reflexively. However, the ensemble of the system and its model move historically, that is, with the arrow of time. The forward movement can be simulated as a recursive routine, while the reflexive subroutine operates incursively, that is, as a feedback against the arrow of time.

In this contribution, I shall show that a differentiated system of communications can be expected to contain two anticipatory mechanisms: (1) meaning is provided with hindsight, i.e., with a time-step difference from the reflected operation in both differentiated and undifferentiated systems; and (2) differentiation in the social system generates an asynchronicity (Δt) between the operation of its differently codified subsystems at each moment in time. The codes of the subsystems provide them concurrently (in the present) with representations of each other. For example, the state of the art in a technology is reflected in prices on the market. The historical development of the technology follows a dynamics which is in important respects different from the price mechanism (Rosenberg, 1976). The two subdynamics, however, can be expected to interact.

When two anticipatory mechanisms operate on each other, a so-called “strongly anticipatory system” can be shaped as the result of a resonance or a coevolution between the two subdynamics. While weakly anticipatory systems contain a model of themselves—which can be used by the system as a prediction—a strongly anticipatory system is also able to rewrite itself. Thus, a differentiated system of communication can endogenously generate mechanisms for its reconstruction. For example, this system can be reconstructed in a techno-economic evolution.

Incursive subdynamics operating upon each other may also lead to hyper-incursion. Knowledge, for example, further codifies the meaning in communication. The formula for the hyper-incursion indicates an uncertainty in the decision-rule which can be appreciated as the need for organization at the interfaces. The knowledge base of the system and its subsystems (e.g., the economy) is based on adding this third subdynamic to the system. The globalizing knowledge base can be expected to rest on a relatively stabilized knowledge infrastructure.

2. Meaning and anticipation as systems operations

In addition to his inheritance of Parsons’s (1937, 1951) repertoire of systems theory,^[1] one can recognize in Luhmann’s writings a relation with American pragmatism and with systems and operations research as other semantic resources. First, the proposal to consider “meaning” (Sinn) as the operator of social systems refers to a central assumption in symbolic interactionism: inter-human interaction generates meaning in a social situation (Blumer, 1969; Lindesmith et al., 1975; Mead, 1934; cf. Luhmann, 1997, at pp. 205 ff.). In this sociological elaboration of the pragmatist tradition and with equal reference to Weber as in the systems tradition, “meaning” has been considered as the constitutive operator that distinguishes the domains of the social sciences from the natural and life sciences. While the latter define their objects naturalistically, in the social sciences one approaches the objects of study reflexively. Schutz (1951), for example, analyzed the codes of communication in a social system when one is “making music together.” However, the systems approach was never appreciated from the perspective of symbolic interactionism (Grathof, 1952; Grant, 2003).

A third tradition which resounds in social systems theory is the quantitative one that roots systems theory in operations research and simulation studies. At several places Luhmann refers to the modeling efforts in systems research. For example, when discussing the relative autonomy of the sciences as subsystems of communication within society, he noted that the closure of the subsystem “science” can be understood from the epistemological perspective as a condition for scientific progress, but that this perspective does not exhaust the advantages of the systems-theoretical description. Luhmann (1990, at p. 340) formulated the additional perspective as follows:

The differentiation of science as an autonomous, operationally closed system using a binary code for its operations is not only a historical “self-realization” of science. Indeed, one is able to describe this process from the perspective of scientific progress. […] However, the theme of relative autonomy based on functional differentiation provides options for further development within the sciences in addition to the philosophical reconstruction. The differentiation of science in society changes also the social system in which it occurs, and this can again be made the subject of scientific theorizing.

Developing this perspective, however, is only possible if an accordingly complex systems theoretical arrangement is specified. It remains the case that the sciences can only communicate what they communicate; science observes according to its own procedures. This is also the case when considering questions about the social system that encompasses the science system. However, when one analyzes the social system as a differentiated system, one can also reflexively consider science as one of its subsystems. From this external perspective the sociologist can study the sciences scientifically and compare their development with other subsystems of society. ^[2]

How can such “an accordingly complex systems-theoretical arrangement” be constructed? How can one move from the theoretical reflection to a model specified in terms of systems operations? Would the specification of such a model of a complex system enable us to run simulations? (Kron, 2002)

Although Luhmann disclaimed the standard methodologies of the social sciences, he saw a key role for methodological developments from this perspective. In his opinion, theoretical programs cannot be further developed without the intervention of methodological programs. For example, Luhmann (1990, at p. 413f.) formulated:

In order to validate the binary code that distinguishes true from false, one needs programs of a different type. Let’s call them methods.

Programmatically, methods provide the perspective that the system lost when it was codified in binary terms. The methods force the specification of the observation in terms of levels and therefore the specification of second-order observations, that is, observations of previous observations by the same system. […] The methodology enables us to formulate programs for a historical machine.^[3]

However, this methodological reflection requires the specification of the problems in a language more formal than the theoretical language. Theories and methods have first to be distinguished and then to be recombined (ibid., p. 428). Among Luhmann’s students, Dirk Baecker has been most prominent in attempts to use George Spencer Brown’s (1969) Laws of Forms for the formalization of the theory.^[4]

Following Von Foerster, Pask, and other systems theoreticians (cf. Glanville, 1996), Baecker (2002) distinguished between two types of models. First-order models aim at improving the quality of theoretical statements about observations, but second-order models consider the first-order descriptions as operating within the systems under observation. For example, scientists report on their observations in the scientific literature, and these reports can again be observed. Consequently, one can attribute the uncertainty in second-order observations to two sources of error: the first-order observations and/or the reflections on these observations. The causality thus becomes “undetermined” and the system under study can therefore be considered “non-trivial.”

For example, if one provides a dually-layered system—processing both information and menaing—with an input, it can be expected to produce an output on the basis of two operations in parallel. The two parallel operations can additionally interact with each other. Thus, a whole range of outputs becomes possible on the basis of a single input. The output is no longer dependent on the input only, but also on the path of the processing of the signal through the complex system. Furthermore, the processing of meaning on top of the information exchange generates meaningful (that is, new) information that can recursively be communicated within the system and then again be provided with meaning. The system under study develops an internal dynamics in addition to its observable behaviour in terms of transforming inputs into outputs (Leydesdorff, 2001a).

The task of a methodological program would be to provide us with tools to distinguish between the two (or more?) levels operating, and their interaction effects, and thus to clarify the operation of a second-order observation by developing the noted “accordingly complex systems-theoretical arrangement.” This task is theoretically urgent because the “undetermined determinateness”—as Baecker calls the non-trivial machine—leads to a paradox that lames the empirical analysis and tends to shift the discourse to the epistemological level. Luhmann (1993, 1999) and Baecker (1999, 2002) have discussed the problem of this paradox of observation mainly with reference to George Spencer Brown (1969). Hans Ulrich Gumbrecht (2003) recently argued in a critical appraisal of Luhmann’s legacy that the focus on the epistemological paradox leads to discussions which fail to add new insights to the well-known problem of the hermeneutic circle in the philosophy of language.

It will be argued here that the paradox can be solved by changing the perspective from a time-independent logic to the time-dependent approach of simulation studies. By using simulations one can consider the phase space of possible combinations of the various subdynamics (e.g., the internal recursion and the transformation of input into output). The geometrical perspectives can then be appreciated as discursive windows on the systems under study but from different (potentially orthogonal) angles and/or at different moments in time. An algorithmic reformulation provides us with means to solve these puzzles because the incommensurabilities among the perspectives can be considered as a consequence of the geometrical metaphors that were used in the narratives. In other words, the computer code enables us to process more complexity than the theoretical language.

3. Specification of the machinery

Let me follow Baecker (2002) for the initial formalization. The author proceeded by using Luhmann’s central notion of a system as an operation that distinguishes the system itself from its environment. An observation is defined by Luhmann (1984, 1997) as a distinction between a system and its environment; the system is thereby identified. Following Von Foerster (1963a and b), the dual operation of identification and distinction is formalized by Baecker (2002, at p. 86) in two steps. First, the system is specified as a distinction between itself and its environment in a functional relationship:

S = f (S, E) (1)

In the second step, the system is operationally closed by attributing the functionality of the distinction to the system itself. One then obtains an identification as follows:

S = S (S, E) (2)

This identity, however, generates the noted paradox because the system can oscillate between a tautology [S = S(S)] and a paradox [S = S(E)]. In the formula, S represents both a system and an operator. The system is thus both self-referential and continuously perturbed by its environment.^[5] However, a system cannot be in both these states at the same time and also be identified. Baecker called this—following similar formulations by Luhmann—the “undecided self-determination” of the system.

In other words, given this paradox, the social system no longer contains a “self” which can be identified unambiguously. Under the condition of functional differentiation the identification can even be codified in a variety of (potentially orthogonal) dimensions. Two elements can thus be added to the formalization. First, because the identification cannot be solved for the two referents at the same time—either a tautology or a paradox is generated—time subscripts must be attributed to the different factors in the equation. Secondly, the differentiation of the social coordination into subsystems has to be appreciated in the formalization. For example, the environment for a subsystem can be another subsystem of the social system. This further complicates the analysis.

Let us first write the time subscripts into Equation 2, as follows:

S_t = S (S_t-1, E_t-1) (3)

This system at a next moment in time S_t is a result of its own operation S on a distinction between its previous state S_t-1 and its environment E_t-1. (The operator S is not provided with a time subscript because the recursive function is codified, and therefore one may expect it to be more stable over time than the substantive communication ons which it operates.) At each time step, the operator synchronizes the past operation of the system with its past environment into the currently emerging state.

Let us now add that the social system is also differentiated into a set of subsystems s₁, s₂, ….., s_n. (I will use the lower case s for the subsystemic level.) Luhmann, in my opinion, has wished to argue that under the condition of functional differentiation the operation of the social system can increasingly be considered as a result of the interactions among social subsystems. In this historical configuration, the environment remains only an external referent that disturbs the self-organization among the subsystems.

Each subsystem processes the same formula at its level when distinguishing between itself and its environment using its specific code c. However, when the formula is specified at the subsystemic level, the environment has to be replaced with other subsystems. One can therefore formalize the configuration as follows:

s_t = s_c (s_t-1, E_t-1) (4)

S_t = S (s₁, s₂, ….., s_n, ε) (5)

Note that the subscript c in the function s_c refers to the specifically coded operation of the subsystem in a given case. The operator can again be expected to be less time-dependent than the development of the subsystem itself. The subsystem develops in terms of variation along its own axis using its codification as a selection mechanism. The environment E of the previous equations is reduced in the above notation to a disturbance term ε.

If the environment is no longer considered external to the social system, but as one or more other subsystems, this has consequences also for the time subscripts in the equations. For example, when a new technology enters the market, the newness of the technology can only be defined with reference to its previous state (t-1), but the market operates as selection pressure on this technology in the present (t). A price is set in terms of current supply and demand, and—in more sophisticated cases—expectations about further technological developments. However, the code of the market is different from the one internal to the development of the technology. Thus, the economy operates in the present by using a representation of the historical development of the technology over time when making, for example, a price/performance comparison in its own terms.

The relations between subsystems are formally symmetrical, but when the codes are different the symmetry in the relations is broken. The systems have a window upon one another, but develop according to their own dynamics in parallel. At the other side of the interface between technologies and markets, a (de-)selected technology may be further developed while taking market perspectives into consideration, but these anticipations are introduced into the engineering only as external referents, that is, in terms of representations using the code of the technological production system. The representations are coded in the code of the receiving (that is, representing) subsystem.

A representation can be considered as a model of the represented system. The model, however, is constructed and entertained by the representing system. The model enables the representing system to reduce the complexity of the represented system. This selection mechanism operates in the present, while each subsystem can only operate using its own code with reference to its previous state. For example, the market operates as a selection mechanism on the variations among the commodities and the technologies. The price mechanism appreciates the alternatives in the present, independently of their historical origins. Vice versa, the market develops historically, but not in relation to the potentially asynchronous development of alternative technologies because the latter develop along their respective trajectories (Dosi, 1982; Nelson and Winter, 1982; Leydesdorff and Van den Besselaar, 1994).

In terms of the model system the replacement of the relation between a system S_t and an environment E_t-1 with a subsystem s_t that relates to other subsystems in its environment thus implies that the time subscripts have to be formulated as follows:

sⁱ _t = sⁱ _c (sⁱ _t-1, s^j _t, … sⁿ _t, ε) (6)

Each subsystem i develops according to its own subdynamics using its code c, but the distinction between this recursive development and the development of other subsystems is made not with reference to the other subsystem’s history, but in terms of a representation at the present moment t. Note that this formula contains a paradox different from the previous one. While the previous paradox was of an epistemological nature, the paradox in this model can be investigated algorithmically for potential solutions. For example, under specifiable conditions two subsystems may begin to coevolve along a trajectory in a techno-economic system. One can consider this as a resonance between different subdynamics.

In summary, the functionally differentiated system develops in terms of models of both the history and the present states of different subsystems. Dubois (1998) proposed distinguishing between the recursion on a previous state sⁱ _t-1 and the incursion of one subsystem on another in the present. In general, a system that contains a model of itself as a subsystem can be considered anticipatory (Rosen, 1985). Models of anticipatory systems were first developed in mathematical biology, but have been elaborated more recently in computational mathematics (Dubois, 2000).

The anticipatory character of the above model can be made more explicit by moving the model one time-step ahead using the following rewrite (of Equation 6):

sⁱ _t = sⁱ _c (sⁱ _t-1, s^j _t, … sⁿ _t, ε) (6)

sⁱ _t+1 = sⁱ _c (sⁱ _t, s^j _t+1, … sⁿ _t+1, ε) (7)

Thus, the next stage of the subsystem is dependent not only on its current state, but also on the (expected) future state of the subsystems in its environment. As noted, each subsystem contains a representation of the other subsystems only as an expectation.

In other words, the subsystems reproduce themselves by solving the puzzle generated by the above specified paradox. The puzzles can be solved because of the orientation on other subsystems in an anticipatory mode. It can be noted that the solution of the paradox remains a consequence of the functional differentiation because this assumption went into the derivation of the formula. Let us now investigate some conditions under which the anticipatory equations can be solved.

4. Anticipatory systems

Anticipatory systems were first defined in mathematical biology by Robert Rosen in his book carrying this title with the ambitious subtitle “Philosophical, mathematical and methodological foundations.” Rosen (1985) defined an anticipatory system as a system that contains a model of itself. This leads to a paradox because the model of the system contains another model of the system, etc. (Kauffman, 2001). I shall now proceed by showing how this paradox can be solved for the undifferentiated system in a manner that differs from the solution to the differentiated case.

In general, the possibility of anticipation is based on using time as a degree of freedom. The clock time of the modeling system runs faster than the clock of the system itself. Therefore, it can anticipate on a future state of the reflected system. The times axis is locally inverted; the modeling system provides meaning to the system under observation from the perspective of hindsight. Thus, the system lags on its representation in the model and is therefore differentiated over time. Once this differentiation is successfully stabilized, a hierarchical control system can be developed within the system. The representation then provides the system with a prediction of its next stage. This anticipatory property can have evolutionary advantages in terms of survival value because an anticipating system has a degree of freedom to adapt proactively its phenotype, that is, before changes in the environment actually occur. Mental models, for example, function in this mode of weak anticipation.

In addition to generating meaning over time the social system contains an anticipatory mechanism at each moment in time because of its functional differentiation. The interaction between anticipation over time with the structural anticipation in the differentiation can provide us with a strongly anticipatory system. Unlike a weakly anticipatory system, a strongly anticipatory one not only makes a prediction of its environment, but reconstructs its configuration and relevant environments continuously (Dubois, 2000). Thus, the operation can be closed at the systems level. The frictions among subsystems operating in parallel within the context of a single (social) system provide the subsystems with another degree of freedom in the synchronization.

An anticipatory system that develops as a function of its historically previous state and its current state, can be formalized as follows:

x_t+1= f(x_t, x_t+1) (8)

For example, one can rewrite the logistic equation in an anticipatory mode. The discrete form of this equation is well-known as:

x_t+1= a * x_t* (1 - x_t) (9)

This equation has been used extensively for modeling, among other things, the growth of a population as a single, i.e., undifferentiated, system. The feedback term (1 - x_t) inhibits further growth of the population represented by x_tas the value of x_t increases over time. This “saturation factor” generates the bending of the well-known sigmoid growth curves of systems for relatively small values of the parameter (1 < a < 3). (For larger values of a, the model bifurcates (at a >= 3.0) or increasingly generates chaos (3.57 < a < 4).)

The anticipatory analogon of this equation can be formulated as follows:

x_t+1= a * x_t* (1 - x_t+1) (10)

In this formulation the growth of the system is no longer constrained by a feedback from the past, but by a feedback in the present. As noted above, one expects the market to feedback on the growth of a technology in the present. Thus, this model fits our previous problem formulation. But we still have to account for the differentiation.

At the subsystemic level, the anticipatory formulation of the logistic model in Equation 10 improves on the previously provided formulation for the differentiated system (Equation 7) because the feedback term is no longer defined in terms of the other subsystems (s^j ….. sⁿ), but as the anticipated representation of the selecting subsystem within the operating subsystem (x) itself. The subsystem develops historically in relation to its previous state (x_t), but this development is reflected in a second process that contains a future-oriented representation of the options and constraints of the subsystem in the next stage (1 – x_t+1). The subsystem is provided by itself with a representation of the selection environments (that is, other subsystems) within this subsystem. This internal representation feeds back as a selection mechanism on the variation generated historically.

Although Rosen’s model was developed for understanding control in hierarchically organized systems, it can thus be provided with another interpretation on the assumption that the system S is differentiated into subsystems (s_i, ….., s_n). Functionally differentiated systems are not synchronized ex ante, but ex post, that is, by their interaction. Thus, the subsystems potentially differ with a Δt ex ante, and this time difference can be considered as a structural form of anticipation. Additionally, the meaning processing can be considered as an anticipation over time.

Note that meaning processing does not require functional differentiation. Meaning processing can be defined at the level of general systems theory. For example, a single mind can also be expected to exhibit “weak” anticipation. However, a social system is able to use two forms of anticipation. When these two forms of anticipation can be brought into resonance, an eigendynamic or self-organization can be developed in an anticipatory layer of the system or, in other words, a knowledge base can be generated (Leydesdorff, 2003a).

So long as the social system is not yet differentiated, the feedback at the system-environment distinction can come only from the environment of the system. However, the system would have no access to its environment other than in terms of its previous, i.e. historical, experiences. This coupling of a system with its environment can be considered as the evolutionary mechanism of structural coupling (Maturana, 1978). In a differentiated system, however, subsystems already belong structurally to the same system. Thus, they do not need to be structurally coupled to one another. They operate in parallel and synchronize in terms of their interactions operationally (ex post). This operational coupling can be made functional to the reproduction.^[6] Since all subsystems are expected to update periodically by using their specific code, one may expect cycles with different frequencies to emerge from these couplings. Without anticipation over the time axis, such a system would tend towards chaos when more than two subdynamics are involved (Schumpeter, 1939; Leydesdorff and Etzkowitz, 1998).

In other words, two subdynamics (e.g., an anticipatory and a reproductive one) can co-evolve in a process of mutual shaping (which may imply relational hierarchization), but a further differentiation into three or more subdynamics changes the evolutionary mechanism. In addition to mutual relations the three subsystems can be expected to develop positions in the relations among one another (Burt, 1982).^[7] Emerging order is then based on synchronization among the subdynamics at specific moments in time and on reflexive anticipation along the time axis within each of the subsystems. The subsystems not only communicate horizontally in terms of functions (Luhmann, 1990, at pp. 635 ff.), but also along the time axis in terms of the frequencies of the updates (Leydesdorff, 1994a).

5. The simulations

One can consider the anticipatory formulation of the logistic equation as a paradox, indeed. An endless recursion can be generated by replacing x_t+1 in the right-hand term of the equation with the entire formula after the equation sign, as follows:

x_t+1 = a * x_t * (1 – x_t+1) (10)

x_t+1 = a * x_t * [1 – a * x_t * (1 – x_t+1)]

etc.

However, this series (unlike some other and comparable ones) happens also to have an analytical solution as can be seen from the following rewrite:

x_t+1 = a * x_t * (1 – x_t+1) (10)

x_t+1 = a * x_t – a * x_t * x_t+1

x_t+1 + a * x_t * x_t+1 = a * x_t

x_t+1 * (1 + a * x_t ) = a * x_t

x_t+1 = a * x_t / (1 + a * x_t) (11)

The model of Equation 11 can again be simulated and the results show properties very different from the logistic map. For example, this map does not exhibit chaotic behaviour at a = 4. Because Lim_x→∞ {ax/(1+ax)} = 1 the anticipatory model always leads to a transition (as in the case of a < 3.0 when using the logistic model). The introduction of an anticipatory mechanism in the model strongly dampens the production of disorder. In general, a representation reduces the variation.

The anticipatory formulation of the logistic equation enables us, among other things, to simulate the generation of an observer within a historically developing system. Figure 1, for example, shows the print of a screen that is divided into two halves. Using a cellular automaton, the bottom half of the screen shows the development of a recursively developing networked system that follows the time axis historically. The update of the top level screen is based on applying the anticipatory version of the logistic equation to the corresponding pixels in the bottom-level screen (by using Equation 11).

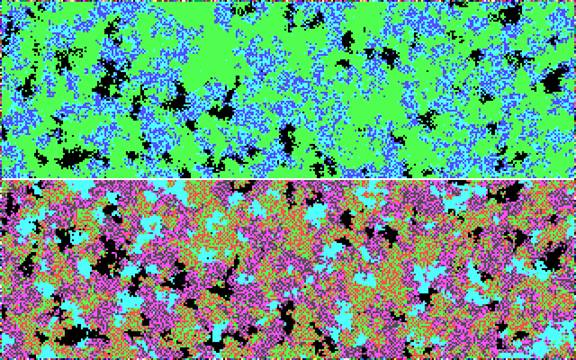
Figure 1. The top-level screen produces a representation of the bottom-level one by using an anticipatory algorithm

In other words, the top-level screen first observes the lower level one. Secondly, the distinction is identified using the observing systems code. Remember that the coding (s_c) was modeled above (Equation 6 in Section 2) as the time-independent parameter of the equation. This corresponds to the parameter a in Equations 10 and 11. By varying this parameter, one can change the specific perspective—that is the selective code—of the observing system, for example, in terms of what can be observed by this system and what cannot. Thus, observer-specific “blind spots” can be generated. Figure 2 provides an example for two different values of the parameter.

Figure 2: Two observing systems with different “blind spots”

In this figure the right-side observer is able to observe more alterations in grey (yellow and red) in the underlying screen than the left-side observer. However, the left-side observer is specifically able to distinguish the darker shades (in pink and brown), while the right-side observer cannot distinguish between the various alterations in grey shades. Thus, the two observers have different blind spots.

The differences between these two observing systems can perhaps not be fully appreciated in grey shades, but the interested reader may wish to run the simulations interactively at http://www.leydesdorff.net/anticipation (Leydesdorff, 2003c). Note that these simulations only take the first step in simulating a social system by generating an observing system that accords with the formal definitions provided by Luhmann. This definition abstracts from an observing agent, and allows observations to be socially distributed a priori (Leydesdorff, 2004).

It can be shown analytically that the assumption of social relatedness as a sole variable among groups of agents provides sufficient basis for deriving the anticipatory formulation of the logistic map as a first-order approximation of the social system (Leydesdorff and Dubois, 2004). This proof could be derived for anticipation in both the interaction term and the aggregation among subgroups of a population. However, the same formula was used in studies of the spread of infectious diseases (Dubois and Sabatier, 1998). Changes in belief systems (e.g., paradigms) have also been modeled in terms of epidemics (e.g., Sterman, 1985, 1999), but this meta-biological perspective does not yet sufficiently appreciate the complexity caused by the reflexivity in inter-human communication (Leydesdorff, 2000).

I shall now proceed by arguing that the reflexive dimension of inter-human communication systems adds another (that is, second) anticipatory mechanism to the first one which was grounded above in the functional differentiation of the social system. The two anticipatory mechanisms—that is, the one based on functional differentiation at each moment in time and the other based on reflexivity along the time axis—can be expected to operate upon each other in a coevolution. Some selections can then be selected for the stabilization of culture (meaning processing), as distinct from the natural processing of information (with the time axis). Thus, both functional differentiation and reflexivity are conditional for the anticipatory generation and processing of meaning at the level of a complex (that is, differentiated) social system. The recombination of these two mechanisms may make the anticipation so strong that the social system can sometimes be reconstructed in terms of a technological evolution (Leydesdorff, 2002a). Without a reflexive recombination, however, disorder would be expected to prevail in a fully differentiated system.

6. The social system as a strongly anticipatory system

The functional differentiation provided us with a first time-difference because of the asynchronicity prevailing between subsystems operating in parallel at each moment in time. Meaning, however, is provided with hindsight, that is, over the time axis, in all systems and subsystems that process meaning. When meaning is generated in a differentiated mode (that is, under the condition of functional differentiation), it operates in all these subsystems by using the time axis orthogonally to the structural differences in codification between and among the subsystems. Thus, the meaning processing in the social system is affected by the differentiation, notably because the meaning is codified differently in the various subsystems. However, the processes in the different subsystems remain formally analogous because the generation and processing of meaning is a systems operation.^[8] It is argued here that the interaction between the two anticipatory mechanisms (the structural one and the temporal one) can transform the system from a weakly anticipatory system into a strongly anticipatory one.

Dubois (2000) proposed a further distinction between “weakly anticipatory systems” and “strongly anticipatory systems.” A weakly anticipatory system contains only a model of the system within the system. This system thus entertains an internal prediction of its relation with the environment, and it is therefore able to anticipate in terms of its behaviour. A strongly anticipatory system, however, uses the anticipation for the construction of its own next stage. In this latter case anticipation can no longer be considered as similar to prediction.

Social systems reconstruct reality in terms of the meaning that is provided to the system (Bhaskar, 1997, 1998). While information is processed historically, that is, following the time axis, meaning is provided to the information exchange from a hindsight (a posteriori) perspective. Meaning processing therefore adds an evolutionary feedback mechanism to the system that inverts the time axis locally.

Note that this operation of generating meaning is not dependent on the systems level. Meaning generation only assumes the stability of an axis along which the incoming (Shannon-type) information can be appreciated. This axis can be stabilized either at the systems level as a hierarchical control mechanism or at the differentiated level of subsystems as specific codes that control the respective subdynamics. By using an axis as another dimension for the projection, some information can be discarded as noise while other information is appreciated as meaningful (Brillouin, 1962; Leydesdorff, 1994b). Bateson (1973, at p. 489), for example, defined meaningful information—that is, information that informs us—as “a difference that makes a difference” (cf. Luhmann, 1984, at p. 103).

Figure 3. The incursive processing of meaning interacts with the recursive processing of information and the result is the production of meaningful information

Whether or not the codification is differentiated, does not yet affect the mechanism of meaning production per se. A hierarchically organized system processes meaning for its integration. In the differentiated case, however, the anticipatory mechanism contained in meaning production may begin to interact with the anticipatory mechanism contained in the differentiation. The meaning is then not only to be generated, but must also be positioned. This positioning is specified in Luhmann’s theory as codification according to the function of the subsystem. Meaning processing enables us additionally to reposition the information across interfaces. As noted, these interfaces can be expected to contain another time difference. The interaction between the two anticipations potentially globalizes the meaning processing beyond the stabilizations (e.g., borderlines) that could provisionally be shaped locally. Hence, the local borders between systems and environments can be expected to develop into interfaces with functions for the next-order or globalized systems of expectations. The borderlines can then also be changed reflexively.

Providing information with meaning can be considered as a selective operation because the noise is discarded. Thus, the meaning processing structures the information processing. Meaning processing continuously reflects on the systems of information processing under observation, but in an evolutionary (that is, with hindsight) mode. The two processes of meaning and information processing can be considered ‘structurally coupled’ within the social system: at the level of the social system, each process cannot operate without the other. At the interface, meaningful information is generated as part of the information processing. Meaning can be further refined into knowledge on the side of the meaning processing.

While biological systems can provide meaning to information, they cannot exchange the meanings thus generated among themselves because they cannot be expected to develop meaning into codified meaning or discursive knowledge that can be exchanged. Thus, they are able to retain (that is, to reproduce) a first-order codification in the hardware, but not a second-order one of providing meaning with specified (that is, knowledge-based) meaning. Maturana (1978), for example, distinguished between the generation of biological observers within the networks and human super-observers who are able to use the language of biology as a science for studying biological processes.

The psychological system is expected not only to process meaning, but also to generate identity. Thus, the anticipation is towards hierarchical control at a center. Unlike the social system—which remains distributed by definition—the dynamics at the level of the individual identity can under certain conditions become historically fixed. Only the social system—Luhmann sometimes used the word “dividuum” as against an individuum—can entertain all these degrees of freedom at the same time. Globalization of meaning can be realized historically when the processing of meaning is not only variable but also differentiated in terms of the codes of the communication.

The reflections at the level of the social system provide us with mirror images. However, under the condition of functional differentiation, one expects variously codified perspectives. When the various reflections can again be communicated, they can recursively be built into the historical (that is, forward) development of the social system. The exchange of meaning adds selectively to the information processing in terms relevant for the reproduction of the social system of communications. Each communication leads to new communications and to new filtering, and thus the social system continuously reconstructs its order of expectations from a hindsight perspective by operating on the layers that it has generated historically (Urry, 2003).

In summary, the social system contains two anticipatory mechanisms: (1) meaning is provided with hindsight, i.e., with a time-step difference from the reflected operation, and can therefore be considered as anticipatory; and (2) the differentiation generates an asynchronicity between the operation of the subsystems which allows for another anticipatory mechanism. Note that the individual mind operates equally in terms of providing meaning, but it cannot reproduce the differentiation structurally as at the level of the social systems. Meanings can be functionally different at the level of an individual, but eventually this system is centered in a hierarchical self, however weak this may be. The social system, however, can process the meaning in different directions and thus this system gains another degree of freedom in the anticipation.

The co-evolution of two anticipatory mechanisms enables the social system to construct its own future. The subsystems use codes to select among the possible meanings historically and in an anticipatory mode. This selection is not synchronized (since differentiated), but the periodicity of the updates induces cycles in the system. By operating upon each other some meanings can be privileged as “knowledge” at the subsystems level. Knowledge can be considered as a meaning that makes a difference.

For example, within the science system one expects the development of discursive knowledge with a dynamics different from idea generation and knowledge-based intuitions at the actor level. However, other subsystems can also be expected to contain second-order codifications (albeit in orthogonal directions). For example, the economy can develop price/performance comparisons as a more complex codification than the price mechanism. Performance comparisons can be considered as an assessment of the technological state-of-the-art in economic terms other than prices.

7. The generation of new dimensions of codification

In a formal representation (Figure 4a), the two subdynamics of ‘representing’ and ‘represented’ can be considered as orthogonal axes informing each other through the covariation in the representation. When the covariation is repeated over time, a coevolution between the two subdynamics may lead to a ‘lock-in’ (Arthur, 1994). In the dynamics of a coevolution the representing/represented dimensions can be expected to alternate in a process of “mutual shaping” (McLuhan, 1964). However, when the emerging system develops further and stabilizes into a third dynamics, one expects non-linearities and therefore the emergence of chaotic behaviour (e.g., crises), unless a mechanism for the synchronization can also be specified.

Figure 4a: Representation as the mutual information (covariation) between the representing and the represented system at each moment in time.

Figure 4b: Evolving systemness in a representation using time as another (third) dimension (z-axis)

The production of a new systems dimension can be explained in terms of the so-called diffusion-reaction system (Rashevsky, 1940; Turing, 1952; Rosen, 1985: 182 ff.). The crux of this rather technical argument is that the two (sub)systems can first “lock-in” into each other (as in a coevolution) when developing increasingly over time (Figure 4b). However, the co-evolution of two subsystems becomes unstable when the diffusion parameter becomes relatively larger than the internal processing rate.^[9] Thus, while the two systems couple first in a coevolution, the expectation is that a bifurcation may occur and a third axis can become independent.^[10] In other words, the coevolution is unstable in the longer run, but it can be considered as a stabilization over considerable stretches of time (Leydesdorff, 2001b and 2002a). Thus, the organizational layer provides the next-order system with mounting blocks that may be left behind as the system further develops.

Arthur (1988, 1989, 1994) modeled the historical development of a “lock-in” using the Polýa urn process. In this process one additional ball of the same colour is placed back in the basket after previously drawing a ball with this colour. Thus, the network develops a historical momentum. For example, the QWERTY keyboard can be analyzed in terms of network externalities, dynamics of scale, and path-dependencies (David, 1985; cf. Liebowitz and Margolis, 1999).

For example, a computer shop can be expected to replenish its supplies when it sells specific brands. The sales pattern of the previous period can become reinforced by the adjusted offering at a next moment in time. Over time, this leads to a profile corresponding to the market segments that are locally most attractive. When supply and demand match, the system of two subsystems (technology and market) can be stabilized in a steady state of the fluxes. For example, the transaction costs can then be minimized. However, when demand increases further, the market may become segmented or otherwise differentiated. The stability gained previously meta-stabilizes in this case and then potentially globalizes.^[11]

The second-order (e.g., temporal) codification of the first-order (e.g., structural) codification can be considered as knowledge generation within the system. Thus, a higher-order dynamics of self-organization can be shaped increasingly within a system of meaning processing. Meaning processing at the individual level provides the resources from which this system “lives,” but the social system is not alive. It does not operates in life-cycles, but in generational cycles that can exhibit a complex pattern of interaction to the extent that the phenotype can also be chaotic (Schumpeter, 1939). The expected information content of the distributions is crucial. Both the sum of the individual contributions and the interaction terms are important for the further developments.

Has the peak in the noise already been developed into a signal which can be picked up by a subsystem in the environment? If so, the noise can be further filtered in a next-order lock-in and co-evolution. The continuous filtering of the noise both between the subsystems and over time provides us with a cultural level of anticipation as a strong—and even hyperselective (Bruckner et al., 1994)—filter on the chaos because it reconstructs itself not only in an adaptive mode, but in an anticipatory mode. These filters, however, remain fragile and fragmented, since socially constructed.^[12] The reconstruction of the system, for example, in terms of new technologies can be expected to remain failure-prone. The new meanings provided in the discourse will be further informed when new knowledge becomes available. Thus, one expects periodical reconstructions of the various meanings and their codifications.

8. Hyper-incursion, decisions, and organization

As the subsystems become increasingly differentiated, their interactions may gain momentum as a (sub)dynamic beyond the control of individual agents or institutional agency. In a differentiated system, the structural coupling between specific agency and structure will be stronger at some places than at others. The resulting subdynamic can be shielded against interventions by agents who are not included in a specific communication. The functional differentiation is retained in the system as institutional structure and thus also as barriers of access to the communication.

For example, non-scientists cannot be expected to participate meaningfully in a scientific discourse that uses a highly codified jargon. The ordinary citizen has specific roles in a political system (e.g., as a member of the electorate), while some people also have executive power. The conditions under which the fluxes can be organized (e.g., by using institutional arrangements) and potentially made the subject of interventions can be distinguished from the level of the self-organizing fluxes (e.g., paradigms in scientific developments or global markets). The next-order level is no longer only agent-based, but network-based, and then increasingly driven by the symbolic coding developed at a next-order level.

How can one model the operation of meaning upon meaning of a different kind at an interface? The incursion upon incursion may induce hyper-incursion. A hyper-incursive anticipatory system can be defined as an incursive anticipatory system generating multiple iterations at each time step (Dubois and Resconi, 1992). Hyper-incursion, therefore, can be expected to have multiple solutions (Dubois, 1998, 2003).

The hyper-incursive formulation of the logistic equation is as follows:

x_t = ax_t+1 (1 – x_t+1) (13)

This system no longer contains a historical reference to its previous state x_t-1, but the next state is a function of different expectations about the future operating upon each other in the present.^[13]

Equation 13 can be rewritten as follows:

x_t = ax_t+1 (1 – x_t+1) (13)

x_t = ax_t+1 – ax_t+1²

ax_t+1² – ax_t+1 + x_t = 0

x_t+1² – x_t+1 + (x_t/a) = 0 (14)

For a = 4, x_t+1 can mathematically be defined as a function of x_t as follows:

x_t+1 = ½ ± ½ √ (1 – x_t) (15)

Depending on the plus or the minus sign in the equation, two future states can thus be generated at each time step. Since this formula is iterative, the number of future states doubles with each next time step. After N time steps, 2^N future states are possible. For N = 10, the number of options is larger than one thousand.

Let me quote Dubois (2003, at pp. 114f.) when he specified the consequences:

This system is unpredictable in the sense that it is not possible to compute its future states in knowing the initial conditions. It is necessary to define successive final conditions at each time step. As the system can only take one value at each time step, something new must be added for resolving the problem. Thus, the following decision function u(t) can be added for making a choice at each time step:

u(t) = 2 d(t) – 1 (8)^[14]

where u = +1 for the decision d = 1 (true) and u = –1 for the decision d = 0 (false). […] It is important to point out that the decisions d(t) do not influence the dynamics of x(t) but only guide the system which creates itself the potential futures.

In a social system, one can expect more options than only true or false. Decisions, however, can be formalized in terms of decision rules like the relatively simple rule specified in the citation. Luhmann (2000) noted that decisions provide the social system with a mechanism for being organized reflexively. This allows for formal organization in addition to informal organization. The latter (informal organization) can be considered as the historical stabilization of patterns of interactions. Formal organization, however, presumes a reflexive turn (Luhmann, 1964, 1978, 2000).

The specific role of organization is to reduce the complexity in the self-organization of the social system. By taking decisions about a perspective for organizing the system under study one reduces the complexity by one degree of freedom. One creates a focus or—in other words—a geometrical representation that can be stabilized. For example, in the above case the ambiguity in choosing either the plus or the minus sign is resolved at each instance and therefore a concrete trajectory is shaped. The idea that the study of social systems requires the specification of a perspective can be traced back to Weber (1904). It is crucial to the social-scientific enterprise: one needs a model for accessing the complexity.

In the case of a complex dynamics, the reduction of the complexity—by maintaining a perspective diachronically or by using organization synchronously—enables us to establish a relational order. A relational order is by definition hierarchical. The center of the representation can also be considered as a focus. When this order (organization) can be stabilized over time, it may become institutionalized, for example, in a corporation or a state apparatus. Note that the natural sequencing of decisions with the flow of time already reduces the self-organization of the system so that it is forced to develop along a trajectory, that is, to develop a history at the systems level independent of whether this situation is reflected in further decisions about stabilizing the organization along the time axis. The reflection adds organization to the series of actions.

At the individual level, one can consider taking action as a first reduction of complexity (Luhmann, 1984, at p. 419; 1995, at p. 308f). Without reflection, action can be based on ‘natural’ preferences (as in the case of the ‘homo economicus’). When action is elaborated into institutional agency or principal agency, organization can be expected to play an increasing role in fulfilling the performative function of action. At the social systems level, the coordination of actions induces organization by taking decisions. From a functional perspective, organization can be considered as the subdynamic that is needed for the maintenance and reproduction of the social system of communications:

Organizations generate possibilities for decisions which otherwise would not have been provided. They use decisions as contexts for decisions. […] As a result an autopoietic systems is thus shaped that distinguishes itself because of its specific form of operation: it generates decisions on the basis of decisions. Behaviour can then be considered as a decision. […] The past is uncoupled by the construction of alternatives. (Luhmann, 1997, at pp. 830f.)^[15]

In the biological model, decisions can be taken ‘naturally’ and under selection pressure. In the sociological model, however, decisions internalize the options. Action can be considered as the primitive (undifferentiated) form of this selection. While action is performative and therefore integrates the options (however irreflexive this decision may be), decisions can be made ever more knowledge-intensive by organizing the relevant interfaces.

9. The algorithmic experience

Discursive theories provide codifications of the meanings operating in the systems under study, but the latter are expected to develop further. Under the condition of functional differentiation, the generation and processing of meaning in scientific discourses has proliferated exponentially (Price, 1961). Because of the recursions and incursions implied, the dissipation of these meanings transforms society and its subsystems at an increasing speed.

The measurement of communications which develop as fluxes at the network level on top of the instantiations which have developed historically requires an algorithmic turn. This algorithmic turn adds reflexivity to the substantiveness of sociological theorizing. When the system processes both self-fulfilling and self-denying expectations, the counter-intuitive results enable us also to improve the knowledge base, but this cannot be controlled by an individual at the top of a hierarchy (Beck, 1992; Fukuyama, 2002). The knowledge-base of social systems is therefore increasingly self-organizing, that is, beyond control of any of the subsystems (Leydesdorff, 2001a; Beck et al., 2003). The fluxes of the events are carried by the structures that were shaped historically. However, the fluxes contain the anticipations.

Luhmann’s program of social systems theory can be read as an expression of this algorithmic experience in systems research. For example, as he formulated it in an essay entitled “The Modernity of Science”:

Knowledge serves—as does, in a different way, art—to render the world invisible as the “unmarked state,” a state that forms can only violate not represent. Any other attempt must be content with paradoxical or tautological descriptions (which is meaningful as well).

[…] The soundness of this reflection, however, arises—and this can still be ascertained by this reflection—from a form of social differentiation that no longer allows for any binding, authorative representation of the world in the world or of society within society. (Luhmann, 2002: 74f.)

A representation which is not reflexively understood as a representation leads to a paradox. An identification in terms of observables is premature because of the uncertainty involved. The codification might then fail to appreciate the provisional character of the distinction which has to be resolved over the time axis. The sociological categories refer to expectations and not to facts with an ontological status. The provisional stabilizations by theorizing, however, remain needed because they reduce the otherwise overwhelming uncertainty. They are based on reducing the algorithmic complexity to the stability of a geometry that can be represented using language (Luhmann, 1997, at pp. 205 ff.; Leydesdorff, 2001a).

The meaning processing from different perspectives can further be codified in terms of potentially incommensurable paradigms (Kuhn, 1962; Leydesdorff, 1994c). From an algorithmic perspective, however, the theorizing reduces the uncertainty only as a heuristic along the time dimension. While the geometric metaphors reduce the complex dynamics under study by one degree of freedom, each selection makes it possible to formulate a perspective and then also a research design. The corresponding stabilization is reflected in the simulation model as the proposal for an equation.

Without the equations, the phase space of the simulation cannot be specified. The equations provide us with both the relevant dimensions—potentially different in the various equations—and their relations, and therefore they enable us to hypothesize that certain states and transitions are more likely than others. When these unlikely events do yet happen to occur within a subsequent run of the simulation, then one’s theoretical assumptions may have to be revised. The distinction between true/false has thus been put to the test. The results, however, can be interpreted from different perspectives (given the differentiation of the communication). One can change either the interpretation or the codification. Human languages provide us with interpretative flexibilities in providing meaning to information (Quine, 1962; Hesse, 1984; Leydesdorff, 1997b).

It seems to me that in this respect the methodological perspective of the algorithmic approach enables us to move beyond Luhmann in terms of our philosophy of science. While Luhmann insisted on the binary character of the code (e.g., true/false), the methodologist also entertains notions like “unlikely” or “less probably true.” The distinction true/false can be considered as epistemological from this perspective because the notion of “less” or “more true” statements presumes this distinction. From an algorithmic perspective, one can use such observations for the specification of an expectation, but one can no longer expect an unambiguous identification. The system of representations loops through its next-order testing before anything can be identified as an outcome. For example, when designing an airplane, one has to tinker endlessly with degrees of freedom in possible designs (Frenken, 2000; Frenken and Leydesdorff, 2000). The computer model appreciates the current state as only one among a variety of possible states.

return

References

Abramson, N. (1963). Information Theory and Coding. New York, etc.: McGraw-Hill.

Aczel, P. (1987). Lectures in Nonwellfounded Sets. CLSI Lecture Notes, 9.

Arthur, W. B. (1988). Competing Technologies. In G. Dosi, C. Freeman, R. Nelson, G. Silverberg, and L. Soete (Ed.), Technical Change and Economic Theory (pp. 590-607). London: Pinter.

Arthur, W. B. (1989). Competing Technologies, Increasing Returns, and Lock-in by Historical Events. Economic Journal, 99, 116-131.

Arthur, W. B. (1994). Increasing Returns and Path Dependence in the Economy. Ann Arbor: University of Michigan Press.

Baecker, D. (Ed.) (1999). Problems of Form. Stanford: Stanford University Press.

Baecker, D. (2002). Wozu Systeme? Berlin: Kulturverlag Kadmos.

Barwise, J., & L. Moss. (1991). Hypersets. Mathematical Intelligencer, 13 (4), 31-41.

Bateson, G. (1972). Steps to an Ecology of Mind. New York: Ballantine.

Beck, U., W. Bonns, & C. Lau (2003). The Theory of Reflexive Modernization: Problematic, Hypotheses and Research Program, Theory, Culture & Society, 20 (2), 1-33.

Bhaskar, R. (1997). On the Ontological Status of Ideas, Journal for the Theory of Social Behaviour, 27(3), 139-147.

Bhaskar, R. (1998). Societies. In M. Archer, R. Bhaskar, A. Collier, T. Lawson, and A. Norrie (Eds.), Critical Realism: Essential Readings (pp. 206-257). London/New York: Routledge.

Blumer, H. (1969). Symbolic Interactionism. Perspective and Method. Englewood Cliffs: Prentice Hall.

Brillouin, L. (1962). Science and Information Theory. New York: Academic Press.

Brown, G. S. (1969). Laws of Form. London: George Allen and Unwin.

Bruckner, E., W. Ebeling, M. A. J. Montaño, and A. Scharnhorst. (1994). Hyperselection and Innovation Described by a Stochastic Model of Technological Evolution. In L. Leydesdorff and P. v. d. Besselaar (Eds.), Evolutionary Economics and Chaos Theory: New Directions in Technology Studies (pp. 79-90). London: Pinter.

Burt, R. S. (1982). Toward a Structural Theory of Action. New York, etc.: Academic Press.

David, P. A. (1985). Clio and the Economics of QWERTY. American Economic Review, 75, 332-337.

Dosi, G. (1982). Technological Paradigms and Technological Trajectories: A Suggested Interpretation of the Determinants and Directions of Technical Change. Research Policy, 11, 147-162.

Dubois, D. M. (1998). Computing Anticipatory Systems with Incursion and Hyperincursion. In D. M. Dubois (Ed.), Computing Anticipatory Systems, CASYS – First International Conference (Vol. 437, pp. 3-29). Woodbury, NY: American Institute of Physics.

Dubois, D. M. (2000). Review of Incursive, Hyperincursive and Anticipatory Systems -- Foundation of Anticipation in Electromagnetism. In D. M. Dubois (Ed.), Computing Anticipatory Systems CASYS’99 (Vol. 517, pp. 3-30). Woodbury, NY: Amercian Institute of Physics.

Dubois, D. M. (2003). Mathematical Foundation of Discrete and Functional Systems with Strong and Weak Anticipation. In M. V. Butz, O. Sigaud, and P. Gérard (Eds.), Anticipatory Behavior in Adaptive Learning Systems. Lecture Notes in Computer Science 2684. Heidelberg: Springer.

Dubois, D. M., and G. Resconi. (1992). Hyperincursivity: A New Mathematical Inquiry. Liège: Presses Universitaires de Liège.

Dubois, D. M., and Ph. Sabatier (1998). Morphogenesis by Diffuse Chaos in Epidemiological Systems, In D. M. Dubois (Ed.), Computing Anticipatory Systems CASYS – First International Conference (Vol. 437, pp. 295-308). Woodbury, NY: American Institute of Physics.

Frenken, K. (2000). A Complexity Approach to Innovation Networks. The Case of the Aircraft Industry (1909-1997). Research Policy 29(2), 257-272.

Frenken, K., and L. Leydesdorff. (2000). Scaling Trajectories in Civil Aircraft (1913-1970). Research Policy, 29 (3), 331-348.

Fukuyama, F. (2002). Our Posthuman Future: Political Consequences of the Biotechnology Revolution. New York: Farrar Straus & Giroux.

Georgescu-Roegen, N. (1971). The Entropy Law and the Economic Process. Cambridge, MA: Harvard University Press.

Glanville, R. (Ed.) (1996). Heinz von Foerster, a Festschrift. Systems Research, 13 (3), 191-432.

Goguen, J. A., and F. J. Varela. (1979). Systems and Distinctions: Duality and Complementarity. International Journal of General Systems, 5, 31- 43.

Grant, C. B. (2003). Complexities of Self and Social Communication. In C. B. Grant (Ed.), Rethinking Communicative Interaction. Amsterdam/Philadelphia: John Benjamins.

Grathoff, R. (Ed.). (1978). The Theory of Social Action. The Correspondence of Alfred Schutz and Talcott Parsons. Bloomington and London: Indiana University Press.

Gumbrecht, H. U. (2003). What Will Remain of Niklas Luhmann's Philosophy? A Daring (and Loving) Speculation. Paper presented at The Opening of Systems Theory Conference, Copenhagen, 23-25 May 2003.

Hesse, M. (1980). Revolutions and Reconstructions in the Philosophy of Science. London: Harvester Press.

Jensen, S. (1978). Interpenetration—Zum Verhältnis Personaler und Sozialer Systeme? Zeitschrift für Soziologie, 7, 116-129.

Kampmann, C., C. Haxholdt, E. Mosekilde, and J. D. Sterman. (1994). Entrainment in a Disaggregated Long-Wave Model. In L. Leydesdorff and P. v. d. Besselaar (Eds.), Evolutionary Economics and Chaos Theory: New Directions in Technology Studies (pp. 109-124). London/New York: Pinter.

Kauffman, L. H. (2001). The Mathematics of Charles Sanders Pierce. Cybernetics & Human Knowing, 8 (1-2), 79-110.

Kron, T. (Ed.). (2002). Luhmann Modelliert: Sozionische Ansätze zur Simulation von Kommunikationssystemen. Opladen: Leske & Budrich.

Kuhn, T. S. (1962). The Structure of Scientific Revolutions. Chicago: University of Chicago Press.

Leydesdorff, L. (1994a). Uncertainty and the Communication of Time, Systems Research, 11, 31-51.

Leydesdorff, L. (1994b). The Evolution of Communication Systems, Int. J. Systems Research and Information Science, 6, 219-230.

Leydesdorff, L. (1994c). Epilogue. In L. Leydesdorff and P. v. d. Besselaar (Eds.), Evolutionary Economics and Chaos Theory: New Directions in Technology Studies (pp. 180-192). London/New York: Pinter.

Leydesdorff, L. (1995). The Challenge of Scientometrics: The development, measurement, and self-organization of scientific communications. Leiden: DSWO/Leiden University; at http://www.upublish.com/books/leydesdorff-sci.htm .

Leydesdorff, L. (1997a). The ‘Post-Institutional’ Perspective: Society as an Emerging System with Dynamically Changing Boundaries. Soziale Systeme, 3, 361-378.

Leydesdorff, L. (1997b). Why Words and Co-Words Cannot Map the Development of the Sciences, Journal of the American Society for Information Science, 48(5), 418-427.

Leydesdorff, L. (2000). Luhmann, Habermas, and the Theory of Communication. Systems Research and Behavioral Science, 17, 273-288.

Leydesdorff, L. (2001a). A Sociological Theory of Communication: The Self-Organization of the Knowledge-Based Society. Parkland, FL: Universal Publishers; at <http://www.upublish.com/books/leydesdorff.htm >.

Leydesdorff, L. (2001b). Technology and Culture: The Dissemination and the Potential 'Lock-in' of New Technologies. Journal of Artificial Societies and Social Simulation, 4 (3), Paper 5, at <http://jasss.soc.surrey.ac.uk/4/3/5.html>.

Leydesdorff, L. (2002a). Some Epistemological Implications of Semiosis in the Social Domain. Semiotics, Evolution, Energy, and Development (SEED) Journal, 2 (3), 60-83; at http://www.library.utoronto.ca/see/SEED/Vol62-63/62-63%20resolved/Leydesdorff.htm .

Leydesdorff, L. (2002b). The Complex Dynamics of Technological Innovation: A Comparison of Models Using Cellular Automata. Systems Research and Behavioural Science, 19 (6), 563-575.

Leydesdorff, L. (2003a). The Construction and Globalization of the Knowledge Base in Inter-Human Communication Systems. Canadian Journal of Communication, 28 (3), 267-289.

Leydesdorff, L. (2003b). The Mutual Information of University-Industry-Government Relations: An Indicator of the Triple Helix Dynamics. Scientometrics, 58 (2), 445-467.

Leydesdorff, L. (2003c). Anticipatory Systems and the Processing of Meaning: A Simulation Using Luhmann's Theory of Social Systems. Paper presented at the European Social Simulation Association (SimSoc VI workshop), Groningen.

Leydesdorff, L. (2004). The Biological Metaphor of a (Second-order) Observer and the Sociological Discourse, Kybernetes (in preparation).

Leydesdorff, L., and P. v. d. Besselaar (Eds.). (1994). Evolutionary Economics and Chaos Theory: New Directions in Technology Studies. London and New York: Pinter.

Leydesdorff, L., and P. v. d. Besselaar. (1998). Technological Development and Factor Substitution in a Non-Linear Model. Journal of Social and Evolutionary Systems, 21, 173-192.

Leydesdorff, L., and D. M. Dubois. (2004). Anticipation in Social Systems. Int. J. of Computing Anticipatory Systems (forthcoming).

Leydesdorff, L., and H. Etzkowitz. (1998). The Triple Helix as a Model for Innovation Studies. Science and Public Policy, 25 (3), 195-203.

Leydesdorff, L., and M. Meyer. (2003). The Triple Helix of University-Industry-Government Relations: Introduction to the Topical Issue. Scientometrics, 58 (2), 191-203.

Liebowitz, S. J., and S. E. Margolis (1999). Winners, Losers & Microsoft: Competition and Antitrust in High Technology. Oakland, CA: The Independent Institute.

Lindesmith, A. R., A. L. Strauss, and N. K. Denzin. (1949, ⁴1975). Social Psychology. Hinsdale: Dryden.

Luhmann, N. (1964). Funktion und Folgen formaler Organisation. Berlin: Duncker & Humblot.

Luhmann, N. (1984). Soziale Systeme. Grundriß einer allgemeinen Theorie. Frankfurt a. M.: Suhrkamp.

Luhmann, N. (1990). Die Wissenschaft der Gesellschaft. Frankfurt a.M.: Suhrkamp.

Luhmann, N. (1993). Die Paradoxie der Form. In D. Baecker (Hrsg.), Kalkül der Form ( pp. 197-212). Frankfurt a. M.: Suhrkamp. [Engl. translation: Baecker, 1999, pp. 15-26.]

Luhmann, N. (1997). Die Gesellschaft der Gesellschaft. Frankfurt a.M.: Surhkamp.

Luhmann, N. (1999). The Paradox of Form. In D. Baecker (Ed.), Problems of Form (pp. 15-26). Stanford, CA: Stanford University Press.

Luhmann, N. (2000). Organisation und Entscheidung. Opladen: Westdeutscher Verlag.

Luhmann, N. (2002). The Modernity of Science. In W. Rasch (Ed.), Theories of Distinction: Redescribing the Descriptions of Modernity (pp. 61-75). Stanford, CA: Stanford University Press.

McLuhan, M. (1964). Understanding Media: The Extension of Man. New York: McGraw-Hill.

Mead, G. H. (1934). The Point of View of Social Behaviourism. In C. H. Morris (Ed.), Mind, Self, & Society from the Standpoint of a Social Behaviourist. Works of G. H. Mead (Vol. 1, pp. 1-41). Chicago and London: University of Chicago Press.

Nelson, R. R., and S. G. Winter. (1982). An Evolutionary Theory of Economic Change. Cambridge, MA: Belknap Press of Harvard University Press.

Parsons, T. S. (1937). The Structure of Social Action. Glencoe, IL: The Free Press.

Parsons, T. S. (1951). The Social System. New York: The Free Press.

Quine, W. V. O. (1962). Carnap and Logical Truth. In Logic and Language: Studies dedicated to Professor Rudolf Carnap on the Occasion of his Seventieth Birthday (pp. 39-63). Dordrecht: Reidel.

Price, D. de Solla (1961). Science since Babylon. New Haven: Yale University Press.

Rashevsky, N. (1940). Bull. Math. Biophys., 1, 15-20.

Rosen, R. (1985). Anticipatory Systems: Philosophical, mathematical and methodological foundations. Oxford, etc.: Pergamon Press.

Rosenberg, N. (1976). The Direction of Technological Change: Inducement Mechanisms and Focusing Devices. In Perspectives on Technology (pp. 108-125). Cambridge: Cambridge University Press.

Schmitt, M. (2002). Ist Luhmann in der Unified Modeling Language darstellbar? Soziologische Beobachtung eines informatischen Komminkationsmediums. In T. Kron (Ed.), Luhmann Modelliert: Sozionische Ansätze zur Simulation von Kommunikationssystemen. (pp. 27-53). Opladen: Leske & Budrich.

Schutz, A. (1951). Making Music Together. Social Research, 18 (1), 76-97.

Sterman, J. D. (1985). The Growth of Knowledge: Testing a Theory of Scientific Revolutions with a Formal Model. Technological Forecasting and Social Change, 28 (2), 93-122.

Sterman, J. D. (1999). Path Dependence, Competitions, and Succession in the Dynamics of Scientific Revolutions. Organization Science, 10 (3), 322-341.

Stewart, I., and J. Cohen. (1997). Figments of Reality: The Evolution of the Curious Mind. Cambridge/New York: Cambridge University Press.

Theil, H. (1972). Statistical Decomposition Analysis. Amsterdam/ London, North-Holland.

Turing, A. M. (1952). Philos. Trans. R. Soc. B., 237, 5-72.

Urry, J. (2003). Global Complexity. Cambridge, UK: Polity Press.

Von Foerster, H. (1993a). Für Niklas Luhmann: Wie rekursiv ist Kommunikation? In: Teoria Sociologica, 2, 61-85.

Von Foerster, H. (1993b). Über selbstorganisierende Systeme und ihre Umwelten. In S. J. Schmidt (Ed.), Wissen und Gewissen: Versuch einer Brücke (pp. 211-232). Frankfurt am Main: Suhrkamp.

return

[1] “Luhmann kennt Parsons so gut, daß er ihn jederzeit referieren kann, ohne in den Text zu schauen (leider aber auch ohne die richtigen Texte zu zitieren)” (Jensen, 1978, at p. 122).

[2] “Die Ausdifferenzierung von Wissenschaft als autonomes, operativ geschlossenes System binär codierter Operationen ist nicht nur ein Geschehen der “Selbstverwirklichung” von Wissenschaft. Gewiß, es kann in der Perspektive wissenschaftlichen Fortschritts so beschrieben werden. [...] Damit sind jedoch die Aspekte, die man dem Thema der Ausdifferenzierung von Wissenschaft abgewinnen kann, bei weitem noch nicht erschöpft. Die Ausdifferenzierung verändert auch das System der Gesellschaft, in dem sie stattfindet, und auch dies kann wiederum Thema der Wissenschaft werden.

Das allerdings ist nur möglich, wenn man ein entsprechend komplexes systemtheoretisches Arrangement zugrundelegt. Es bleibt dabei: die Wissenschaft kommuniziert nur das, was sie kommuniziert; sie beobachted nur das, was sie beobachtet, und nur so, wie sie beobachtet. Das gilt auch, wenn sie Fragen des sie umfassenden Gesellschaftssystems behandelt. Behandelt sie die Gesellschaft als differenziertes System, kann sie aber zugleich sich selbst behandeln—sich selbst als ein Subsystem dieses Systems. Sie kann sich, mit diesen ihren eigenen Vorgaben, so betrachten, als ob sie van außen wäre, und sich auf diese Weise mit anderen Subsystemen des Gesellschaftssystems vergleichen.”

[3] “Um den binären Code, die Unterscheidung von wahr und unwahr, zur Geltung zu bringen, benötigt man daher Programme eines anderen Typs. Wir nennen sie Methoden.

Methoden lösen auf der Ebene der Programme das ein, was dem System durch binäre Codierung aufgegeben ist. Sie erzwingen eine Verlagerung des Beobachtens auf die Ebene einer Selbstbeobachtung zweiter Ordnung, auf die Ebene des Beobachtens eigener Beobachtungen. [...] Die Methodologie formuliert Programme für eine historische Maschine.”

[4] For an elaborate formalization of Spencer Brown’s logic see also Goguen & Varela (1979).

[5] This same formula has also been used in hyperset theory. A hyperset H is defined as a collection of its elements E and itself: H = {E, H} (Barwise & Moss, 1991; cf. Aczel, 1987). Dubois (1998, at p. 7) used hyperset theory for his model of anticipatory systems.

[6] Schmitt (2002, at p. 34) has argued that different systems cannot be operationally coupled because then they would not be able to distinguish themselves in terms of their operations. In accordance with Luhmann’s theory, he argues that systems can be coupled structurally, but they remain operationally closed. As noted above, the relation system/environment changes when the system of reference is functionally differentiated into subsystems. Functionally differentiated subsystems are both operationally closed and dependent upon one another, for example, with reference to the reproduction of the next-order system. The operational closure in this case can be considered as a tendency that allows for the processing of more complexity at the systems level. However, the subsystems also communicate in terms of providing functions for each other. According to Equation 7, a subsystem relates to itself and to other subsystems of the same system as its relevant environments. Thus, this form of coupling is (one order) more complex than in the case of structural coupling (Leydesdorff, 1994a, 2001).

[7] When three subdynamics are involved, the mutual information in three dimensions (that is, the probabilistic entropy generated in the relations) can under certain conditions become negative (Abramson, 1963: 129f). Using empirical data, I could show in another context that the mutual information in three dimensions can become negative when the data is both interactive (e.g., co-occurs) and the interaction can be considered codified (Leydesdorff, 2003b). In a differentiated system the network of relations spans an architecture that potentially reduces the uncertainty among the actors locally. Since the mutual information in three dimensions can also be positive, the balance between the two modes of operation (agent-based versus communication-based) remains empirical. The dynamics of the system can only shift from agent-based to communication-based when the generation of variation at the network level is larger than the variation produced at the nodes.

[8] Meaning can be specified at the level of general systems theory; information can be defined mathematically, that is, without reference to a system (Leydesdorff, 2003a).

[9] The formal condition is that the diffusion parameter D is larger than the rate constant a divided by two. The one eigenvalue of the matrix representing the two coupled systems then becomes positive, while the other is negative. A saddle point is thus generated and a bifurcation in the system is the consequence.

[10] In formulaic format:

f(xy) = a x^α + by^β + c(xy)^γ (12)

If the interaction term (xy) can recursively be stabilized, for example, because of coevolution and/or lock-in, a trajectory can be shaped along a third axis z. While initially developed as a function of the interaction (xy), this axis can increasingly become orthogonal to the interacting systems x and y. Thus, the system can endogenously gain a degree of freedom. When this happens, all mutual informations among x, y, and z can be declared in the next stage. The emergence of a new dimension in the system can be assessed using the Markov property in the coevolution between the two axes x and y as a test, while as argued above the self-organization of the newly emerging system can be measured in terms of the mutual information among the three axes x, y, and z (Leydesdorff, 2003b; Leydesdorff and Van den Besselaar, 1998).

[11] From an historical perspective (that is, with the arrow of time) one would consider this instability as a destabilization, but from an evolutionary perspective (that is, with hindsight) this can be considered as a meta-stabilization because a degree of freedom is gained in the bifurcation. Initially, the bifurcation is fixed as an oscillation, but when the frequency interacts with other bifurcations in a complex system, a more complex dynamics (including the generation of negative entropy in the mutual relations in three or more dimensions) can be expected. Thus, the degree of freedom in the meta-stabilization can be used by a system for its globalization.

[12] All derivatives from “esse” (to be; e.g., ontology) can perhaps be replaced with derivatives from “frangere” (that is, “to break;” cf. Leydesdorff, 1997a; Stewart and Cohen, 1997).

[13] There are two additional formulas which merit investigation:

x_t = ax_t (1 – x_t+1) (16a)

x_t = ax_t+1 (1 – x_t) (16b)

· Equation 16a evolves into x = (a – 1)/a = Constant. I submit that this evolution towards a constant through anticipation can be considered in modeling the self-reference of an (individual) identity.

· Equation 16b evolves into x_t+1= (1/a) {x_t / (1 – x_t)} Since the latter term approaches –1 as its limit value and the former term is a constant (1/a), this representation can alternate between itself and its mirror image. This subdynamic thus formalizes the reflexive operation.

Both these dynamics (that is, Eqs. 16a and 16b) can be expected to play a role in social systems.

[14] The numbering of the equations in the quotation follows the original text.

[15] “Organisationen erzeugen Entscheidungsmöglichkeiten, die es anderenfalls nicht gäbe. Sie setzen Entscheidungen als Kontexte für Entscheidungen ein. […] Im Ergebnis kommt auf diese Weise ein autopoietisches System zustande, das sich durch eine besondere Form von Operationen auszeichnet: Es erzeugt Entscheidungen durch Entscheidungen. Verhalten wird als Entscheidung kommuniziert. […] Die Vergangenheit wird durch die Konstruktion von Alternativen abgehängt.”