The Triple Helix Model and the Knowledge-Based Economy
Loet Leydesdorff [a] & Martin Meyer [b]
Abstract. The Triple Helix model of university-industry-government relations can be generalized from a neo-institutional model of networks of relations to a neo-evolutionary model of how three selection environments operate upon one another. Two selection mechanisms operating upon each other can mutually shape a trajectory, while three selection environments can be expected to generate a regime. The neo-evolutionary model enables us to appreciate both organizational integration in university-industry-government relations and differentiation among functions like wealth creation, knowledge production, and legislation. The specification of systems of innovations in terms of nations, sectors, and regions can then be formulated as empirical questions: is synergy generated among functions in a network of relations? Thus, this Triple Helix model enables us to study the knowledge base of an economy in terms of a trade-off between locally stabilized and (potentially locked-in) trajectories versus techno-economic regimes at the global level.
Keywords: Triple Helix, knowledge-based economy, trajectory, regime, selection, globalization
Introduction
The Triple Helix has been associated with the study of networks of university-industry-government relations. In our opinion, the institutional networks provide only the knowledge infrastructures of knowledge-based systems. A knowledge infrastructure can be considered as an evolving retention mechanism of the fluxes of communication in a complex system of interactions. Beyond this institutional layer, however, the Triple Helix model can be extended to a neo-evolutionary model of how three selection environments can be expected to operate upon one another in terms of functions. The three evolutionary functions required for shaping a knowledge-based economy can be considered as economic wealth generation, organized knowledge production, and normative control.
Three selection mechanisms operating upon one another can be expected to generate complex dynamics (May, 2006; May & Leonard, 1975; Sonis, 2000). In Darwin’s original evolution theory, selection was first considered “natural,” that is, as given by nature. In the paradigm of evolutionary economics (Schumpeter, 1939), different selection environments were distinguished; for example, market as against non-market environments (Nelson & Winter, 1982; Von Hippel, 1988). Comparative studies across different sectors of the economy (e.g., Nelson, 1982; Carlsson, 2002 and 2006; Carlsson & Stankiewicz, 1991) and studies of different national systems of innovation (Lundvall, 1992; Nelson, 1993) have been central to this tradition. However, the analysis of interaction effects among selection environments cannot be pursued without an analytical model.
In the Triple Helix model, selection dynamics are endogenous because actors in the three institutional spheres relate to one another reflexively and in a distributed mode. Thus, they react to each other’s selections. Dosi (1982) noted that the operation of two selection environments upon each other can be expected to generate a trajectory. A specific trajectory can be localized in a space of possible trajectories. Three selection environments can model the global regime of a knowledge-based economy because a degree of freedom is added.
The relation between this evolutionary model of interacting dynamics and the institutional layer of university-industry-government relations is no longer one-to-one. Nevertheless, wealth generation remains institutionally associated with industry, and knowledge production with academia, while control in the public sphere can be associated with government or with management in the private sphere. The interacting dynamics are anchored in differentiations, while network relations can be expected to reflect degrees of integration. Integration and differentiation are concomitant: the functionally differentiated system is able to process more complexity (Luhmann, 1984) and the exchanges make it possible to change perspectives (Giddens, 1981).
For example, universities can sometimes act as regional innovation organizers, corporations have become important producers of new knowledge, etc., but the main missions of industries, universities, and governments remain institutionally (and to a certain extent legally) defined. Thus, one can expect trade-offs and “boundary objects” at the interfaces (Gieryn, 1983; Star & Griesemer, 1989; Galison & Stump, 1995). The three perspectives are interwoven in social phenomena. For example, patents can function in court because they offer legal protection, but they can also be used as indicators of knowledge production and/or economic value (Figure 1).
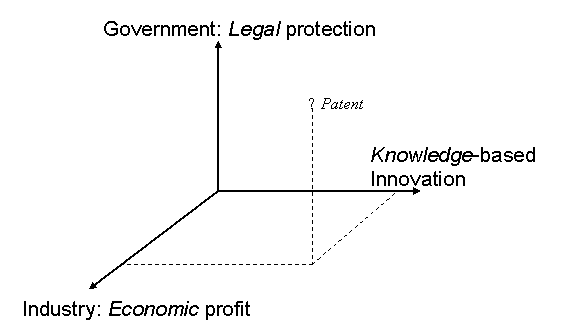
Figure 1: Three functions of patenting
Using this Triple Helix model, one can explain the phenomena in a knowledge-based order by means of a three-dimensional scheme. One can expect more than two contexts to be relevant because discursive knowledge has become a third coordination mechanism at the level of society, in addition to—and in interaction with—economic exchange relations and political control. This additional degree of freedom in the coordination can be considered as the distinguishing feature between a knowledge-based and a political economy (Leydesdorff, 2006).
The network relations are observable, while the functions can be expected to operate as the latent eigenvectors of the networks. In other words, integration can be analyzed as a co-variation in relation to remaining variation in the co-varying, but qualitatively different dimensions. For example, Gómez et al. (2007) illustrated the third mission of the university by providing the following factor matrix of a set of indicators for 65 Spanish universities:
|
|
|
|
Component |
|||
|
|
|
|
1 |
2 |
3 |
4 |
|
No. PhD professors |
|
0.969 |
|
|
|
|
|
No. students |
|
0.921 |
|
|
|
|
|
No. ISI publications |
|
0.874 |
0.404 |
|
|
|
|
No. PhD thesis |
|
0.835 |
|
|
|
|
|
University age |
|
0.673 |
|
|
-0.422 |
|
|
No. students/PhD prof. |
-0.62 |
|
|
|
||
|
No. citations/article |
|
|
0.919 |
|
|
|
|
No. ISI doc/PhD prof. |
|
|
0.868 |
|
|
|
|
% internat. vs. Spanish publications |
|
0.818 |
|
|
||
|
% non-cited articles |
|
|
-0.815 |
|
|
|
|
% doc. in top journals* 10 |
|
0.608 |
0.398 |
|
||
|
Input specialisation (Pratt-PhD prof) |
|
|
0.858 |
|
||
|
GDP of NUTS2 regions |
|
|
0.689 |
0.354 |
||
|
International collaboration rate |
|
0.535 |
0.627 |
-0.415 |
||
|
University-industry collab. Rate |
|
|
|
0.808 |
||
|
National collaboration rate |
|
|
|
0.605 |
||
|
Output specialisation (Pratt‑publicat.) |
-0.31 |
|
0.441 |
0.516 |
||
Table 1: Rotated Component Matrix of
indicators for 65 Spanish universities. Extraction Method: Principal Component Analysis. Rotation
Method: Varimax with Kaiser Normalization. Only loadings larger than 0.3
are shown. Source: Gómez et
al. (2007, at p. 341).
In the context of this discussion, factor 4 (which explains 11.45% of the variance) represents the third mission of the universities. The first and second missions, that is, teaching and research, are indicated by factors 1 (26.49%) and 2 (23.22%), respectively. The third factor (12.49%) indicates a correlation between relatively rich regions (in Spain) and the internationalization of research as measured in terms of coauthorship relations. Factor loadings on factor 4 show that the internationalization of research is negatively correlated with university-industry collaborations in this Spanish context. However, university-industry relations are positively correlated with national collaborations. University-industry relations correlate also positively with regional development and specialization (Ibid., p. 342).
Sun et al. (2007) showed that in the case of Japan, university-industry coauthorship relations have declined continuously since 1980 in terms of co-authorship relations (after normalization). However, since 1994 the Japanese system has developed a new synergy between international co-authorship relations and university-industry-government relations. The uncertainty prevailing at the national level is reduced by this additional synergy (Leydesdorff & Sun, in preparation).
Using the neo-evolutionary Triple Helix model of a dually layered development—that is, in terms of both institutions and functions—it remains an empirical question where and when integration or differentiation will prevail in a given configuration. The opening of China to the world market after the demise of the Soviet Union posed a major threat to the Japanese system, and then the trend towards more international co-authorship among Japanese scientists and scholars (Wagner, 2004, 2008) could be integrated at the level of the national system. Whether integration or differentiation prevails may vary over time and with the systems under study.
The analytical model
In a knowledge-based economy, organized knowledge production and control (Whitley, 1984) has become a third coordination mechanism in addition to the previously existing coordination mechanisms of a political economy: market exchanges and political control (Leydesdorff, 2006). The three functions have to be carried by agency at the nodes, but one can no longer expect a one-to-one correspondence between functions and institutions because the functions are based on network arrangements among the institutions (Etzkowitz & Leydesdorff, 2000). Systemic effects may occur that cannot be traced back directly to specific exchange relations, but emerge at the systems level because of synergy in interactions among functions (Burt, 1995).
The relations between two of the three functions—technological innovation and changes in economic factor prices—could be modeled in evolutionary economics in terms of economically motivated shifts along the production function or innovative shifts of the production function towards the origin (Schumpeter, 1939; Nelson & Winter, 1982; Sahal, 1981). Innovations tend to upset the economic equilibrium (Figure 2).
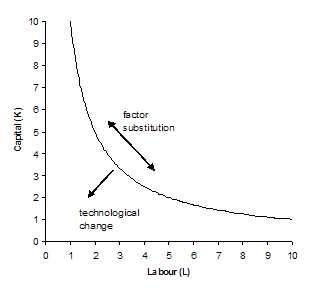
Figure 2: Using the production function (Q = c.K.L), factor substitution and technological change can be distinguished as different subdynamics.
When two functions operate as selection environments upon each other, one can expect mutual shaping between these selection environments along a trajectory (Dosi, 1982; Leydesdorff & Van den Besselaar, 1998a). Stabilization in a local optimum can be considered as an effect of co-evolution between selections in one dimension and another.
Competing stabilizations can also be considered as second-order variations and can further be selected for hyper-stabilization, meta-stabilization, and globalization when a third (analytically independent) selection mechanism can be expected to operate. Hayami & Ruttan (1970) already noted a second-order selection mechanism operating at the global level (Nelson & Winter, 1982). While a trajectory forms a trail along trade-offs, an additional (third) feedback from the environment may induce globalization or a lock-in as a hyper-stabilization. Alternatively, the relatively stabilized trajectory can become meta-stable and bifurcate. The control mechanism then shifts from the local (and potentially stabilized) trajectory to a global next-order or regime level.
Let us model interactions among selection mechanisms using the logistic equation. In this model, a system x grows with reference to its previous state, but it experiences a feedback (1 – x) because of its growth in a competitive environment:
The feedback term (1 – xt) inhibits the further growth of this system as the value of x increases over time. In the case of a techno-economic system, this feedback on the historical variation and growth can be provided by the market as a selection environment.[3] In other words, technological development generates variation on the basis of the previous state of the system (modeled here as axt), but this variation is selected by an increasingly selective environment (1 – xt).
For populations or technologies which compete with one another, the logistic equation can be generalized to the so-called Lotka-Volterra equations in which competition coefficients (α) are added to the selection mechanisms (May, 1973; Sonis, 1992, 2000; Nijkamp & Reggiani, 1994: 98). In both the logistic equation and the Lotka-Volterra equations, selection is modeled as feedback. This feedback (k – αx), in the case of Lotka-Volterra, assuming unity of the parameters and without loss of generality, can be formulated as (1 – x).
Two selections operating on a variation v (v is equal to axt in Equation 1) result in a quadratic expression for the resulting selection environment in the following form:
f(x) = v (1 – x) ( 1 – x) (2)
= v (x2 – 2 x + 1) (3)
This resulting selection environment no longer operates as a homogenous field because it is curved. It can be represented as in Figure 3a (on the left side): a system containing two selections can be stabilized at the minimum of a quadratic curve. When this minimum is extended along the time dimension, a valley is shaped in which the system develops along a trajectory. Sahal (1985: 79) called the resulting shapes “innovation avenue” and compared them with river beds in ecological systems theory (Waddington, 1957).
|
|
|
|
Figure 3a:
|
Figure 3b:
|
Adding one more selection term leads to a complex dynamics (Figure 3b). One can then expect the landscape to be no longer smooth, but “rugged” (Kauffman, 1993).
The inclusion of a third selection environment can be modeled analogously as the following equation:
f(x) = v (1 – x) ( 1 – x) ( 1 – x)
= – v (x3 – 3 x2 + 3 x – 1) (4)
This cubic function is represented above as the dotted line in Figure 3b. As long as the three selection mechanisms operate synchronously on a single variation with the same parameters (in this case all set to unity), the global and stable points of inflection will coincide at a so-called saddle point. In this special case, the historically stabilizable system can remain identical with the global one. One can perhaps consider such a system as containing a single—or Nelson & Winter’s (1982) “natural”—trajectory in which the global optimum coincides with the localized one.
Figure 3b shows—as the line with an arrow—the configuration resulting when stabilization and globalization operate with different parameter values. In this (more general) case the curve can be expected to show both a maximum and a minimum. At the minimum the techno-economic system is locally stabilized, but at the maximum it can be considered as meta-stable. Consequently, a bifurcation is induced: the system can either go backward (to the stabilization at a local optimum) or forward (to globalization into a next-order regime).
As long as the system remains stable (that is, at the minimum), it can further develop along its trajectory hitherto. However, the flux tends to move the system towards the other basin of attraction. This attraction is caused by the possibility to communicate in an additional dimension, and thus to process more complexity in a newly emerging configuration. The local optimum can also be considered as a niche in which the technology can develop momentum to reach the hilltop which separates it from the next basin of attraction. The latter provides a global environment for the local development.
Reaction-diffusion dynamics will be used in a later section for modeling this bifurcation. However, let us first pay attention to the sign of the equation. Equation 3 had a positive sign, and consequently the hyperbola in Figure 3a showed a minimum. If this sign is reversed, a third subdynamic must play a role at the systems level. For formal reasons, the inversion cannot be endogenous to the two selections which co-evolved to stabilize the system at a minimum. The third selection mechanism may either reinforce the prevailing stability and make the system hyper-stable, or invert the sign and make the system meta-stable (Figure 4).
In other words, both meta-stability and hyper-stability indicate that a third subdynamic is operating. For example, a political economy tends towards stabilization because two social coordination mechanisms (economics and politics) interact, while a knowledge-based economy can be expected to exhibit more complex dynamics because a third coordination mechanism (knowledge production) is increasingly taking over control functions (Langford et al., 1997; Leydesdorff & Etzkowitz, 1998).
|
|
|
|
Figure 4: Meta-stabilization (Figure 4a) or hyper-stabilization (Figure 4b) of the techno-economic system in curvatures of a complex selection environment. |
|
For example, the change in the sign of the selection environments between Figures 4a and b can be understood as the difference between a market with decreasing marginal returns and one with increasing marginal returns (e.g., in Arthur’s [1988] case of information and communication technologies). Increasing marginal returns lead to a bifurcation at the meta-stable vertex of the hyperbola and a consequential lock-in on either side. In the case of a lock-in, the previously meta-stable system is thereafter again hyper-stabilized by a feedback that reinforces the co-evolution between the other two subdynamics.
The Knowledge-based Economy and Systems of Innovation
How can the above systems-dynamic considerations help us to understand the observable relations between the major players in the field? From an evolutionary perspective, the networks provide us with footprints of the systems or, more abstractly formulated, representations of the systems dynamics. The functions in the systems under study remain virtual when measured in terms of instantiations. In other words, relevant selection mechanisms can be formulated as hypotheses whereas only the variation can be observed. The formulation of hypotheses relates measurement to theorizing. Among other things, theorizing enables us to designate latent dimensions.
The Triple Helix model emerged in the context of two competing theories: one about (national) systems of innovation (Freeman, 1987, 1988; Lundvall, 1988, 1992; Nelson, 1993) and the second celebrating the “new production of knowledge” or “Mode-2” (Gibbons et al., 1994; Nowotny et al., 2001). The proponents of the “Mode-2” thesis argued that the capitalist system had undergone a radical transition that had changed the mode of knowledge production in its core: disciplinary knowledge would increasingly become obsolete and be replaced by techno-scientific knowledge to be generated in “transdisciplinary” projects.
Whereas the “Mode 2” model focused exclusively on transitions, the concept of a system of innovations, as it prevails in evolutionary economics, suggests the resilience of existing arrangements. Extensive research was done in this tradition, mostly based on systematic comparisons among different innovation contexts (Nelson, 1982, 1993; Lundvall, 1992; Carlsson & Stankiewicz, 1991; Braczyk et al., 1998). In addition to the idea that the nation state as a specific construct of the 19th and early 20th centuries would provide a stable context for the development of national innovation systems, other scholars claimed sectorial or regional frameworks as potential candidates for the stabilizing environments (Carlsson, 2006).
The Triple Helix model explains these differences in terms of possible arrangements. Two of the three dynamics can stabilize along a trajectory when a third context remains relatively constant. Which of the three subdynamics provide this foothold may vary among instantiations and over time. When a technology is leading the trajectory along a stable path, a sectorial system can be expected to emerge (Pavitt, 1984). When governments are able to provide strong regulatory frameworks (as in the People’s Republic of China) one can expect the dominance of a national system of innovation. At the regional level, trade-offs between regional governments, local universities, and industrial capacities may shape specific niches (Cooke & Leydesdorff, 2006).
Sometimes universities can take the lead in developing an area (De Rosa Pires & De Castro, 1997; Etzkowitz et al., 2000). However, one can expect that each niche remains in transition: a region that was able to ride a wave may be in disarray a decade later because, for example, multi-national corporations are able to buy themselves into the innovative trajectories that were stabilized at the level of the region (Beccatini et al., 2003). Dynamics of scale and scope may lead to globalization.
For example, when the nations of Eastern Europe became transition economies after the demise of the Soviet Union in 1991, the ambitions of these countries to develop national systems of innovation met with interference from market forces, on the one hand, and from the ongoing political process of Europeanization, on the other. An interesting example is provided by the case of Hungary (Inzelt, 2004). Not one, but three innovation systems emerged during the transition. A metropolitan center developed around Budapest to compete with Vienna, Munich, Prague, etc., as a seat for knowledge-intensive services, multinational corporations, etc. In the western part of the country, specific Western-European companies moved in to the extent that they were able to influence research agendas at universities. The German car manufacturer Audi, for example, developed its own university institute at a local university in a town and region in North-Western Hungary where it developed an automotive cluster (Lengyel et al., 2006). A third type of innovation system could be indicated in the eastern parts of the country, where traditional universities and urbanizations provide local infrastructures that have remained more continuous with the old system (Lengyel & Leydesdorff, 2007).
In other words, when Hungary arrived on the European scene, it was too late to develop a purely national innovation system because the envisaged system was already implicated in the formation of the European Union. Transition countries became at the same time accession countries for the European Union and the resulting dynamics could henceforth only be coordinated loosely at the national level. The period for adaptation was too short for stabilizing a national system of innovations.
This “disorganization” may vary from country to country and from region to region within countries. In this case, the transition was not only a transition at the trajectory level, but a change at the regime level; the complex dynamics among the interacting selection environments were controlled at the level of the emerging system. This concept of a “system,” however, should not be reified: the interacting distributions determine the dynamics at the regime level. One can no longer expect a stable center where decision-making can be monopolized because the one-to-one correspondence between functions and institutions no longer prevails.
This version of the Mode-2 thesis—that is, the disorganization and fragmentation of previously existing system delineations—is appreciated in the Triple Helix model in terms of a reflexive “overlay” of relations among the carriers of innovation systems (Etzkowitz & Leydesdorff, 2000). The overlay feeds back as a restructuring subdynamic on the underlying networks, and generates and/or blocks opportunities for niche-formation in a distributed mode. New competencies may be needed for these developments; new specialties are shaped as recombinations of existing disciplinary capacities. The dynamics are thus no longer institutional, but evolutionary. The perspective is both with hindsight and forward-looking. The dynamics generate the flexibilities; not as a biological adaptation, but as a social dynamics of intentions (Leydesdorff, 2009).
From this perspective, the flexibilization and contextualization of Mode-2 is no longer confined to the knowledge production and control system (Whitley, 2001). Mergers and acquisitions in industry are increasingly knowledge-driven. The context of the European Union has changed the status of regions, and nation states can be dissolved as in the case of Czechoslovakia, or, continuously reformed, as in the case of Belgium. In the new regime, the system remains in “endless transition” (Etzkowitz & Leydesdorff, 1998). However, this “endless transition” does not mean that “anything goes” (Feyerabend, 1975), but rather a continuous recombination of strengths and competitive advantages under selection pressure (Cooke & Leydesdorff, 2006). This selection process is knowledge-intensive.
The normative implications of the model
Although the model specifies primarily a research agenda, the Triple Helix thesis has also been used for neo-corporatist and neo-liberal agendas of policy making. In terms of innovation policies, however, neo-liberalism and neo-corporatism are not mutually exclusive (Rothwell & Zegveld, 1981). The Swedish state agency for innovation, Vinnova, for example, has made “The Triple Helix” its official strategy (Etzkowitz, 2005, 2008) because this model corresponds with this country’s neo-corporatist traditions (Lehmbruch & Schmitter, 1982). According to others (e.g., Mirowski & Sent, 2007),[4] a further commercialization of the university could result from this “ideology” in liberal democracies.
While the neo-institutional model of intersecting networks may guide the researcher towards instances where university-industry-government relations can be studied empirically, in a neo-evolutionary model the emphasis remains on finding explanations for the dynamics of knowledge-based systems. An absence of relations can be as important as their presence; the focus is on empirical distributions, that is, the observable variations, and the theoretical specification of latent selection mechanisms. Precisely because a one-to-one relation between carriers and functions in a network can no longer be assumed, the relevant contexts have to be operationalized in terms of the functions carried by networked agents.
For example, the “Varieties of Capitalism” debate (Hall & Soskice, 2001) neglected the knowledge production function as an independent source of variance and focused almost exclusively on differences in political economies. Similarly, “best practices” in university-industry relations cannot be transferred among regions because regulatory and legislative conditions—the role of government—can be different (Leydesdorff, 2003). Three instead of two analytically different selection mechanisms are involved in knowledge-based systems: economic equilibrium-seeking, knowledge production, and organizational control.
The Triple Helix model stimulates the researcher to discuss the three functions in a research design and thus to enrich the explanation. For example, Van Looy et al. (2007) showed that the introduction of Bayh-Dole type legislation had an independent effect on patenting by universities when compared among European nations. The increases range from 250% for Germany, or 300% for Belgium, to 500% for Denmark. More detailed analysis in the Belgian case revealed that the university has to ensure that inventive activities do not jeopardize research and education. In addition, each university has to install procedures to ensure a fair return on investment in patenting for researchers and research groups.
The neo-evolutionary version of the Triple Helix model does not prescribe that one “should” collaborate in local networks and in the service of regional development. However, the model suggests that a three-dimensional design is sufficiently complex to analyze the integration and differentiation mechanisms among the subdynamics (Ashby, 1958; Leydesdorff & Fritsch, 2006). One may wish to add more dimensions for the analysis (as in the above mentioned study of Sun et al. (2007); cf. Leydesdorff & Sun, in preparation). However, the analysis of a complex system in terms of a single “co-evolution” between two of the three dynamics underestimates the complexity by focusing on a trajectory of integrations and construction in one stage that may bifurcate at a later stage.
Bifurcation and Evolutionary Change
When a development is hyper-stabilized in a niche, the system is locked-in and not sufficiently able to absorb new variants for its further development; in other words, it has reached the end of an evolutionary cycle (Salthe, 1993). As argued above, this configuration is already (necessarily) based on three interacting selection mechanisms: the third selection mechanism induced the life-cycle into the trajectory.[5] How can a “break-out” from lock-in be considered from the perspective of a model which hypothesizes a third selection environment?
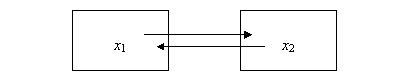
As noted, we can turn to reaction-diffusion dynamics to understand this possibility. Reaction-diffusion dynamics have been elaborated in the natural sciences (Rashevsky, 1940; Turing, 1952; Rosen, 1985, pp.182ff.; Bruckner et al., 1994). If two systems are tightly coupled (as in a co-evolution; see Figure 5), the simplest coupling mechanism can be specified by the following differential equations:
dx1/dt = – ax1 + D(x1 – x2) + S (5a)
dx2/dt = – ax2 + D(x2 – x1) + S (5b)
|
|
|
|
|
|
Figure 5: Two coupled processes (Rosen 1985, p.183).
Let us assume that x is produced in both compartments at a constant and equal rate S. The parameter a represents the decay of x; D is the diffusion constant across the interface. (For the sake of simplicity, these parameters are assumed to be equal on both sides.) The diffusion is asymmetrical depending on the concentrations of x1 and x2 in the two compartments. This system of equations provides values for the steady state at:
x1* = x2* = S/a (6)
The concentrations of x in the two environments are then equal, and the system is homogeneous. However, the operational stability of the system is determined by the eigenvalues of the matrix of the coefficients of x1 and x2 in Equations 5a and 5b. This matrix is:
|
D – a |
– D |
|
– D |
D – a |
The two eigenvalues of this system are:
λ 1 = – a; λ 2 = 2D – a (7)
While the first eigenvalue is always negative, the second can become positive if D > a/2. Thus, if diffusion of x to the other system becomes more important than the flux in the production process (divided by two), both a positive and a negative eigenvalue coexist. The system then becomes unstable because a saddle point is generated in the phase diagram. Any deviation from homogeneity will be amplified, and the system can undergo a phase transition.
A phase transition changes the dynamics of a system irreversibly. In the case of two previously coupled dynamics, the bifurcation leads to a polarization, that is, a situation in which all the materials are either in the one cell or the other. Which sub-dynamic will prevail will depend on the initial (and potentially random) deviation from homogeneity, possibly provided by the third environment. The reaction-diffusion dynamics thus enables us to understand how a lock-in between a single technology and the market dynamics can be dissolved at a later stage: a co-evolution along a single trajectory is “unlocked” when the diffusion mechanism of the market, for instance, no longer co-evolves with the production mechanism.
Production and marketing may co-evolve tightly within an innovative enterprise or an industrial district (Callon et al. 2002). If a smaller production unit is absorbed by a multinational corporation or otherwise internationalized, this tight coupling between production and marketing may constrain further development. Pressure for global diffusion may then allow for reallocation decisions about the techno-economic system, increasingly reshaping the production process. Schumpeter himself made this distinction between the phase of start-up and creative destruction based on low concentration in the market (“Mark I”) and the phase of shake-out and creative accumulation based on high concentration (“Mark II”) in his studies of 1912 and 1942, respectively (Schumpter, 1912, 1942; Nelson & Winter, 1982; Kamien & Schwartz, 1982; Malerba & Orsenigo, 1996).
When another environment becomes a relevant selection environment to a previously locked-in system, the new configuration may begin to tilt the system as soon as diffusion at the new interface becomes more important than (as suggested by Eq. 7) half of the rate along the trajectory of the system. Because an economic production system is attracted by market opportunities, one would expect a trajectory to be exploited to gain market share. The diffusion rate for the technology, therefore, can be expected to increase. A previous lock-in can in this case be expected to erode endogenously the conditions for its existence in the longer term. The feedback arrow is inverted as between Figures 4a and 4b above.
For example, the VHS video recorder was a standard and dominant technology in the 1990s (Arthur, 1988). The CD did not change this, as video material could not be recorded on it. The DVD, however, became increasingly relevant as an alternative, but this did not mean that the lock-in was immediately broken. A prevailing system can be resilient! After a while, however, when the DVD-share had grown independently for other reasons (e.g., due to its superior data storage characteristics), the system tilted and a substitution process generated a cascading away from the VHS towards an entirely new system dynamics. The newly emerging lock-in can be expected to follow the curve of the alternative technology (Leydesdorff & Van den Besselaar, 1998b). In terms of the visualization of Figure 3b and 4a above, the system moves over the hilltop and flows into the other basin of attraction.
In summary, the system may be locked into a suboptimal configuration because the fitness landscape can be rugged (Kauffman 1993; Frenken, 2005). Along a given trajectory this techno-economic system is relatively stabilized against disturbances. When the rugged landscape itself becomes dynamic as a third selection environment, the reaction-diffusion dynamics may open the lock-in. This newly shaped system may, paradoxically, have been a result of the erosion of the previous lock-in of the system, since the system needs to be stabilized before it can enter its next-order globalization.
University Patenting
University patenting has often been considered as an indicator of Triple Helix-type developments. More recently, licensing royalties (e.g., Thursby et al., 2001) and spin-off companies (e.g., Friedman & Silberman, 2003) have been proposed as measures of university involvement in technology commercialization, but the measurement of these proxies is even more complicated than patent statistics (Siegel et al., 2003). Does the decline of university patenting in recent years imply the end of the Triple Helix thesis because of the prevailing identification of the Triple Helix thesis with the rise of “the entrepreneurial university” (Henderson et al., 1998; Etzkowitz, 2002).
Before discussing the issue in terms of the neo-institutional and neo-evolutionary versions of the Triple Helix thesis, let us first provide the data about this relatively recent decline in university patenting.
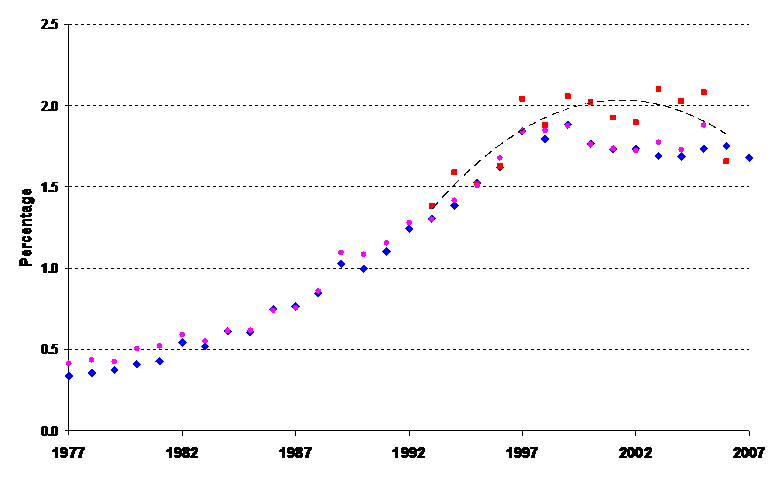
Figure 6: University patenting (1977-2007) as a percentage of patenting in the USPTO database. (Sources: ■ AUTM, 2007; ♦ online search at http://www.uspto.gov, 15 January 2008; ● Wong & Singh (2007).)
Figure 6 is based on three independent sources. The squares (■) indicate the number of university patents (normalized as a percentage of USPTO patents) as listed in the yearly reports of the Association of University Technology Managers (AUTM, 2007); the diamonds (♦) indicate this percentage as measured by searching with the word “university” in the field of the assignees among the patents issued during the period 1977-2007.[6] Wong & Singh (2007) also provided numbers for university patenting in the USPTO database (● ; all universities).
The online indicator omits institutes like MIT that do not have the word “university” in their name. For this reason, Figure 7 provides the results of searching the Esp@ce database for worldwide patenting in four major American universities, among which MIT and CalTech.
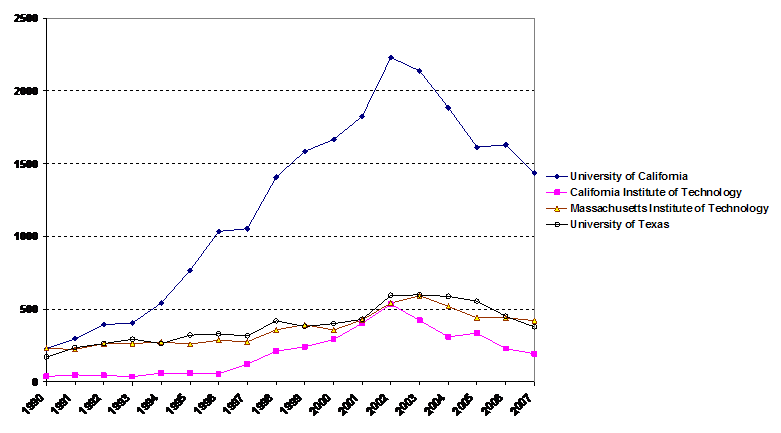
Figure 7: Worldwide patents of four leading US universities. (Source: Esp@ce database;[7] 7 June 2008)
Figure 7 first shows that worldwide patenting in US universities is now at a considerably higher level than domestic patenting despite the “home advantage” effect (Criscuolo, 2006). Within the USPTO database, the University of California—which is an aggregate of eleven universities in California—peaked with 468 patents in 2002, while 2,230 patents could be counted worldwide as the peak in this same year.
Whatever the measurement problems with these different databases may be, the trend is clear and not exclusively American. Figure 8 provides a figure in the same format for four leading non-American universities. (ISIS Innovation was added to the graph for Oxford University because the university uses the services of this bureau for its patenting.)
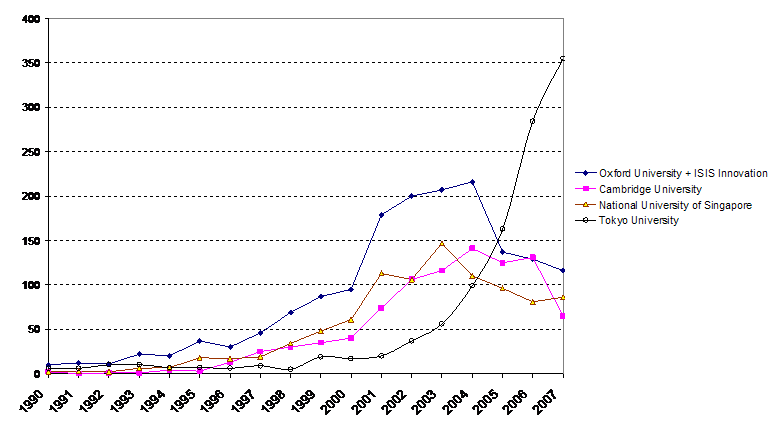
Figure 8: Patenting by leading non-American universities.[8] (Source: Esp@ce database; 7 June 2008).
While all curves exhibit decline or stabilization, Tokyo University is the single exception with an ongoing increase in patenting at an exponential rate. This is probably caused by strong incentives from the national government. Note that patenting by European universities took off only during the 1990s, while the American universities had already increased their (mainly domestic) patenting activities during the 1980s.
The counter-argument that the observed decline is the effect of “institutional learning” by universities is not convincing. Why would it take American universities twenty years to learn that university patenting is expensive and not always rewarding, while this was noted extensively in the relevant literature during the 1990s (Rosenberg & Nelson, 1994; Webster & Packer, 1997; Rappert et al., 1999)? More recently the number of spin-off companies from academic institutions has also declined (Mustar, 2007). Furthermore, this author noted that university incubators entertain decreasing links with the research process itself.
In our opinion, these developments can be appreciated differently. In addition to potential learning effects, the emphasis has changed at the global level, and this has led to a return to core missions of universities. More than before universities are nowadays ranked in terms of their knowledge output, and patents or spin-offs are usually not part of this ranking (e.g., THES, 2007). The nature of the competition among universities is changing. In other words, the current selection environments are interacting differently from these in the previous period. The specification of selection environments has to be updated regularly because each trajectory performs a life-cycle.
Conclusion
The return of universities to core missions does not imply that the Triple Helix thesis has lost its validity from a neo-evolutionary perspective: the system has changed by engaging with its relevant environments no longer in terms of institutional boundaries, but increasingly in terms of functional relations. These are manifested in neo-institutional arrangements that can be shaped and dissolved in collaborations and competitions much more flexibly than before. A new social contract has been shaped between the knowledge-production function in academia and industries and governments as the main partners . Patenting, for example, has become a possible function of universities, albeit not a core one, as the proponents of Mode-2 and the institutional version of the Triple Helix thesis once predicted. The third mission has remained a latent one, including new forms of education, incubation, and long-term commitments to social values.
Our model is inspired by Luhmann’s (1984) reformulation of Parsons’s structural-functionalism (Merton, 1973). The functions are not given axiomatically , but shaped historically as coordination mechanisms, or, in Luhmann’s words: social subsystems of communication that are differentiated in terms of what is mediated and why. The control systems in these communications can be considered as latent functions that operate as codes of the communication (Maturana & Varela, 1980). Among the many possible codes of communication, some have been symbolically generalized more than others. When codes of communication are symbolically generalized, one can expect them to carry different functions (Parsons, 1968).
Economic exchange (“value” on the market place) and political control (“power” and legitimation) took the lead in shaping the political economies of the 19th and 20th centuries. The “wedding of science and the useful arts” (Noble, 1977) in the late 19th century triggered the gradual transition to a knowledge-based economy during the 20th century. This process could only be completed after the end of the Cold War, which was essentially a war about how to organize a political economy.
In a knowledge-based economy, “trading-off” has taken the place of competition for dominance of a specific format. Trade-offs among social coordination mechanisms can be improved by making them more knowledge-based (Galison & Stump, 1995). We have argued that a system with trade-offs along three main axes contains a structural dynamics different from that of a system that is not able to use the third axis (that is, science and technology) flexibly as both a resource and an investment (Latour, 1987). Our neo-evolutionary version of the Triple Helix model enables us to distinguish trajectories and regimes as analytical constructs, and then also to understand “lock-ins” and “break-outs” in relation to models in which these concepts can be provided with meaning. This reflexivity about the crucial role of the model itself raises in turn the question of the functionality of the model.
A model that takes the three structural dimensions of university-industry-government relations into account and no longer contextualizes the cognitive one—either methodologically as an external and potentially neutral “observer” or sociologically and economically as an exogenous driver—enables the analyst to specify the relations between private property and profit maximization, public control functions as legislation and regulation, and the innovative dynamics of the techno-sciences in empirical instances, and thus to contribute to the development of solutions to problems at interfaces among the central functions of today’s society. Indeed, the latter is an interdisciplinary enterprise, but the analytical and empirical tasks are far more specific than in the Mode-2 model. We argue for a focus on analytically and empirically informed de-contextualization and knowledge-based reconstruction at specific interfaces in contrast to Nowotny et al.’s (2001) programmatic emphasis on “strong” contextualizations (cf. Barnes & Edge, 1982).
Acknowledgement
We are grateful for the comments of Andrea Scharnhorst and Wilfred Dolfsma on a previous version of this paper.
References
Aoki, M. (2001). Towards a Comparative Institutional Analysis. Cambridge, MA: MIT Press.
Arthur, W. B. (1988). Competing technologies. In G. Dosi, C. Freeman, R. Nelson, G. Silverberg, & L. Soete (Ed.), Technical Change and Economic Theory (pp. 590-607.). London: Pinter.
Ashby, W. R. (1958). Requisite variety and its implications for the control of complex systems. Cybernetica, 1(2), 1-17.
AUTM (2007). AUTM U.S. Licensing Activity Survey FY 2006. Available at http://www.autm.net/events/file/AUTM_06_US%20LSS_FNL.pdf [Retrieved on December 15, 2007].
Barnes, B., & Edge, D. (Eds.). (1982). Science in Context. Cambridge, MA: MIT Press.
Beccatini, G., Bellandi, M., Ottati, G. D., & Sforzi, F. (2003). From Industrial Districts to Local Development: An Itinerary of Research. Cheltenham, UK; Northampton, MA: Edward Elgar.
Braczyk, H.-J., Cooke, P., & Heidenreich, M. (Eds.). (1998). Regional Innovation Systems. London/ Bristol PA: University College London Press.
Bruckner, E., Ebeling, W., Montaño, M. A. J., & Scharnhorst, A. (1994). Hyperselection and Innovation Described by a Stochastic Model of Technological Evolution. In L. Leydesdorff & P. van den Besselaar (Eds.), Evolutionary Economics and Chaos Theory: New Directions in Technology Studies (pp. 79-90). London: Pinter.
Burt, R. S. (1995). Structural Holes: The Social Structure of Competition. Cambridge, MA: Harvard University Press.
Carlsson, B. (2006). Internationalization of Innovation Systems: A Survey of the Literature. Research Policy, 35(1), 56-67.
Carlsson, B. (Ed.). (2002). New Technological Systems in the Bio Industries -- An International Study. Boston/Dordrecht/London: Kluwer Academic Publishers.
Carlsson, B., & Stankiewicz, R. (1991). On the Nature, Function, and Composition of Technological Systems. Journal of Evolutionary Economics, 1(2), 93-118.
Cooke, P., & Leydesdorff, L. (2006). Regional Development in the Knowledge-Based Economy: The Construction of Advantages. Journal of Technology Transfer, 31(1), 5-15.
Criscuolo, P. (2006). The 'home advantage' effect and patent families. A comparison of OECD triadic patents, the USTPTO and EPO. Scientometrics, 66(1), 23-41.
De Rosa Pires, A., & De Castro, E. A. (1997). Can a Strategic Project for a University Be Strategic to Regional Development? Science and Public Policy, 24(1), 15-20.
Etzkowitz, H. (2002). MIT and the Rise of Entrepreneurial Science. London: Routledge.
Etzkowitz, H. (2005). Trippelhelix – den nya innovationsmodellen. Stockholm: SNS Press.
Etzkowitz, H. (2008). The Triple Helix: University-Industry-Government Innovation in Action. London: Routledge.
Etzkowitz, H., & Leydesdorff, L. (1998). The Endless Transition: A “Triple Helix” of University-Industry-Government Relations, Introduction to a Theme Issue. Minerva, 36, 203-208.
Etzkowitz, H., & Leydesdorff, L. (2000). The Dynamics of Innovation: From National Systems and ‘Mode 2’ to a Triple Helix of University-Industry-Government Relations. Research Policy, 29(2), 109-123.
Etzkowitz, H., Webster, A., Gebhardt, C., & Terra, B. R. C. (2000). The future of the university and the university of the future: evolution of ivory tower to entrepreneurial paradigm. Research Policy, 29(2), 313-330.
Feyerabend, P. (1975). Against Method London: NLB).
Freeman, C. (1987). Technology and Economic Performance: Lessons from Japan. London: Pinter.
Freeman, C. (1988). Japan, a New System of Innovation. In G. Dosi, C. Freeman, R. Nelson, G. Silverberg, & L. Soete (Ed.), Technical Change and Economic Theory (pp. 31-54). London: Pinter.
Frenken, K. (2000). A Complexity Approach to Innovation Networks. The Case of the Aircraft Industry (1909-1997). Research Policy, 29(2), 257-272.
Frenken, K. (2005). Innovation, Evolution and Complexity Theory. Cheltenham, UK/Northampton, MA: Edward Elgar.
Friedman, J., & Silberman, J. (2003). University Technology Transfer: Do Incentives, Management, and Location Matter? The Journal of Technology Transfer, 28(1), 17-30.
Galison, P. L., & Stump, D. (Eds.). (1995). The Disunity of Science: Boundaries, Context, and Power. Stanford, CA: Stanford University Press.
Gibbons, M., Limoges, C., Nowotny, H., Schwartzman, S., Scott, P., & Trow, M. (1994). The new production of knowledge: the dynamics of science and research in contemporary societies. London: Sage.
Giddens, A. (1981). Agency, institution, and time-space analysis. In K. D. Knorr-Cetina & A. V. Cicourel (Eds.), Advances in Social Theory and Methodology. Toward an Integration of Micro- and Macro-Sociologies (pp. 161-174). London: Routledge & Kegan Paul.
Gieryn, T. F. (1983). Boundary-Work and the Demarcation of Science from Non-Science: Strains and Interests in Professional Ideologies of Scientists. American Sociological Review, 48(6), 781-795.
Gómez, I., Bordons, M., Fernández, M. T., & Morillo, F. (2007). Structure and Peformance of Spanish Universities. Proceedings of the 11th International Conference of Scientometrics and Informetrics, D. Torres-Salinas & H. Moed (Eds.), CSIC, Madrid, 21-25 June 2007. Vol. 1, 335-345.
Hall, P. A., & Soskice, D. W. (Eds.). (2001). Varieties of Capitalism: The Institutional Foundations of Comparative Advantage. Oxford, etc.: Oxford University Press.
Hayami, Y., & Ruttan, V. W. (1970). Agricultural Productivity Differences among Countries. The American Economic Review, 60(5), 895-911.
Henderson, R., Jaffe, A., & Trajtenberg, M. (1998). Universities as a source of commercial technology: A detailed analysis of university patenting, 1965-1988. Review of Economics and Statistics, 80(1), 119-127.
Inzelt, A. (2004). The evolution of university–industry–government relationships during transition. Research Policy, 33(6-7), 975-995.
Kamien, M. I., & Schwartz, N. L. (1982). Market Structure and Innovation. Cambridge MA: Cambridge University Press.
Kauffman, S. A. (1993). The Origins of Order: Self-Organization and Selection in Evolution. New York: Oxford University Press.
Langford, C. H., Burch, R. D., & Langford, M. W. (1997). The 'well-stirred reactor': evolution of industry–government–university relations in Canada. Science and Public Policy 24(1), 21-27.
Latour, B. (1983). Give Me A Laboratory and I will Raise the World. In K. D. Knorr-Cetina & M. J. Mulkay (Eds.), Science Observed (pp. 141-170.). London: Sage.
Lehmbruch, G., & Schmitter, P. C. (1982). Patterns of corporatist policy-making. London: Sage.
Lengyel B., Lukács E., Solymári G. (2006). A külföldi érdekeltségű vállalkozások és az egyetemek kapcsolata Győrött, Miskolcon és Szegeden. Tér és Társadalom, 4, 127-140.
Lengyel, B., & Leydesdorff, L. (2007). Measuring the knowledge base in Hungary: Triple Helix dynamics in a transition economy. Paper presented at the 6th Triple Helix Conference, 16-19 May 2007, Singapore.
Leydesdorff, L. (2002). The Complex Dynamics of Technological Innovation: A Comparison of Models Using Cellular Automata. Systems Research and Behavioural Science, 19(6), 563-575.
Leydesdorff, L. (2003). A methodological perspective on the evaluation of the promotion of university-industry-government relations. Small Business Economics, 22(2), 201-204.
Leydesdorff, L. (2006). The Knowledge-Based Economy: Modeled, Measured, Simulated. Boca Raton, FL: Universal Publishers.
Leydesdorff, L. (2009). The Non-linear Dynamics of Meaning-Processing in Social Systems. Social Science Information, 48(1), forthcoming.
Leydesdorff, L., & Etzkowitz, H. (1998). The Triple Helix as a model for innovation studies. Science and Public Policy, 25(3), 195-203.
Leydesdorff, L., & Fritsch, M. (2006). Measuring the Knowledge Base of Regional Innovation Systems in Germany in terms of a Triple Helix Dynamics. Research Policy, 35(10), 1538-1553.
Leydesdorff, L., & Sun, Y. (in preparation). National and International Dimensions of the Triple Helix in Japan: University-Industry-Government versus International Co-Authorship Relations.
Leydesdorff, L., & Van den Besselaar, P. (1998). Technological Development and Factor Substitution in a Non-linear Model. Journal of Social and Evolutionary Systems, 21, 173-192.
Luhmann, N. (1984). Soziale Systeme. Grundriß einer allgemeinen Theorie. Frankfurt a. M.: Suhrkamp.
Lundvall, B.-Å. (1988). Innovation as an interactive process: from user-producer interaction to the national system of innovation. In G. Dosi, C. Freeman, R. Nelson, G. Silverberg & L. Soete (Eds.), Technical Change and Economic Theory (pp. 349-369). London: Pinter.
Lundvall, B.-Å. (Ed.). (1992). National Systems of Innovation. London: Pinter.
Malerba, F., & Orsenigo, L. (1996). Schumpeterian patterns of innovation are technology-specific. Research Policy, 25(3), 451-478.
Maturana, H. R., & Varela, F. (1980). Autopoiesis and Cognition: The Realization of the Living. Boston: Reidel.
May, R. M. (1973). Stability and Complexity in Model Ecosystems. Princeton, NJ: Princeton University Press.
May, R. M. (1976). Simple mathematical models with very complicated dynamics. Nature, 261(June 10), 459-467.
May, R. M., & Leonard, W. J. (1975). Nonlinear Aspects of Competition between Three Species. SIAM Journal of Applied Mathematics, 29(2), 243-253.
Merton, R. K. (1973). The Sociology of Science: Theoretical and empirical investigations. Chicago/London: University of Chicago Press.
Mirowski, P., & Sent, E. M. (2007). The Commercialization of Science, and the Response of STS. In E. J. Hackett, O. Amsterdamska, M. Lynch & J. Wajcman (Eds.), Handbook of Science, Technology and Society Studies (pp. 635-689). Cambridge, MA/London: MIT Press.
Mustar, P. (2007). Public Policies to Foster the Creation of University Spin-Off Firms in Europe: Expectations, Results and Challenges. Paper presented at the 6th Triple Helix Conference, Singapore, 16-18 May 2007.
Noble, D. (1977). America by Design. New York: Knopf.
Nelson, R. R. (Ed.). (1993). National Innovation Systems: A comparative analysis. New York: Oxford University Press.
Nelson, R. R., & Winter, S. G. (1982). An Evolutionary Theory of Economic Change. Cambridge, MA: Belknap Press of Harvard University Press.
Nowotny, H., Scott, P., & Gibbons, M. (2001). Re-Thinking Science: Knowledge and the Public in an Age of Uncertainty. Cambridge, etc: Polity.
Parsons, T. (1968). Interaction: I. Social Interaction. In D. L. Sills (Ed.), The International Encyclopedia of the Social Sciences (Vol. 7, pp. 429-441). New York: McGraw-Hill.
Pavitt, K. (1984). Sectoral patterns of technical change: towards a theory and a taxonomy. Research Policy, 13, 343-373.
Rappert, B., Webster, A., & Charles, D. (1999). Making sense of diversity and reluctance: academic–industrial relations and intellectual property. Research Policy, 28(8), 873-890.
Rashevsky, N. (1940). An approach to the mathematical biophysics of biological self-regulation and of cell polarity. Bull. Math. Biophys., 1, 15-25.
Rosen, R. (1985). Anticipatory Systems: Philosophical, mathematical and methodological foundations. Oxford, etc.: Pergamon Press.
Rosenberg, N., & Nelson, R. R. (1994). American universities and technical advance in industry. Research Policy, 23, 323-348.
Rothwell, R., & Zegveld, W. (1981). Industrial Innovation and Public Policy. London: Pinter.
Sahal, D. (1981). Alternative Conceptions of Technology. Research Policy, 10, 2- 24.
Sahal, D. (1985). Technological guideposts and innovation avenues. Research Policy, 14, 61-82.
Salthe, S. N. (1993). Development and Evolution: Complexity and Change in Biology. Cambridge, MA: MIT Press.
Schumpeter, J. (1912). The Theory of Economic Development. Oxford: Oxford University Press.
Schumpeter, J. ([1939], 1964). Business Cycles: A Theoretical, Historical and Statistical Analysis of Capitalist Process. New York: McGraw-Hill.
Schumpeter, J. (1943). Socialism, Capitalism and Democracy. London: Allen & Unwin.
Siegel, D. S., Waldman, D., & Link, A. (2003). Assessing the impact of organizational practices on the relative productivity of university technology transfer offices: an exploratory study. Research Policy, 32(1), 27-48.
Sonis, M. (1992). Innovation Diffusion, Schupeterian Competition and Dynamic Choice: A new synthesis. Journal of Scientific and Industrial Research 51, 172-186.
Sonis, M. (2000). Nonlinear Socio-Ecological Dynamics and First Principles of Collective Choice Behavior of “Homo Socialis.” Progress of Theoretical Physics, 139(Supplement No. 139), 257-269.
Star, S. L., & Griesemer, J. R. (1989). Institutional Ecology,Translations' and Boundary Objects: Amateurs and Professionals in Berkeley's Museum of Vertebrate Zoology, 1907-39. Social Studies of Science, 19(3), 387.
Sun, Y., Negishi, M., & Leydesdorff, L. (2007). National and International Dimensions of the Triple Helix in Japan: University-Industry-Government and International Co-Authorship Relations. Proceedings of the 11th International Conference of Scientometrics and Informetrics, D. Torres-Salinas & H. Moed (Eds.), Vol. 2, pp. 936f., CSIC, Madrid, 21-25 June 2007.
THES (2007), Times Higher Education Supplement – QS World University Ranking, Times Higher Education Supplement, 8 November 2007; Available at http://www.thes.co.uk/worldrankings/ (Retrieved, 15 December 2007)
Thursby, J. G., Jensen, R., & Thursby, M. C. (2001). Objectives, Characteristics and Outcomes of University Licensing: A Survey of Major US Universities. The Journal of Technology Transfer, 26(1), 59-72.
Turing, A. M. (1952). The Chemical Basis of Morphogenesis. Philosophical Transactions of the Royal Society, Series B, 237, 37-72.
Van Looy, B., Du Plessis, M., Meyer, M., & Debackere, K., The Impact of Legislative Framework Conditions on the Entrepreneurial Activities of Universities: An empirical assessment, Paper presented at the 6th Triple Helix Conference, Singapore, 16-18 May 2007.
Waddington, C. H. (1957). The Strategy of Genes. London: Allen & Unwin.
Wagner, C. S. (2004). International Collaboration in Science: A new dynamic for knowledge creation. Amsterdam: University of Amsterdam.
Wagner, C. S. (2008). The New Invisible College. Washington, DC: Brookings Press.
Webster, A., & Packer, K. (1997). When Worlds Collide: Patents in Public-Sector Research. In H. Etzkowitz & L. Leydesdorff (Eds.), Universities and the Global Knowledge Economy: A Triple Helix of University-Industry-Government Relations (pp. 47-59). London: Pinter.
Whitley, R. D. (1984). The Intellectual and Social Organization of the Sciences. Oxford: Oxford University Press.
Whitley, R. D. (2001). National Innovation Systems. In N. J. Smelser & P. B. Baltes (Eds.), International Encyclopedia of the Social and Behavioral Sciences (pp. 10303-10309). Oxford, UK: Elsevier.
Wong, P. K., & Singh, A. (2007). Patenting by Leading Universities in the World: Link to Quantity and Quality of Scientific Publications. Paper presented at the 6th Triple Helix Conference, Singapore, 16-18 May 2007.
[a] Amsterdam School of Communications Research (ASCoR), University of Amsterdam, Kloveniersburgwal 48, 1012 CX Amsterdam, The Netherlands; loet@leydesdorff.net; http://www.leydesdorff.net.
[b] SPRU, University of Sussex, Brighton, UK; Steunpunt O&O Statistieken, Katholieke Universiteit Leuven, Belgium.
[3] This so-called ‘saturation factor’ generates the bending of the sigmoid growth curves of systems for relatively small values of the parameter (1 < a < 3). For larger values of a, the model bifurcates (at a >= 3.0) or increasingly generates chaos (3.57 < a < 4).
[4] Mirowski & Sent (2007) ironically replace the Triple Helix categories with “Corporate,” “Governmental,” and “Educational” (CGE). In their opinion, CGE fits better in the hegemonial discourse of STS, while the Triple Helix employs a terminology used by “scholars from the periphery.”
[5] The consequent dynamics within a single basin of attraction is consistent with the prediction of rugged fitness landscapes following from Kauffman’s (1993) NK-model (Frenken, 2000; Leydesdorff, 2002).
[6] We used issued patents because patent applications are published only since 2001.
[7] http://ep.espacenet.com/advancedSearch?locale=en_EP . These searches are based on publication years of issued patents. Inclusion in the database may lag on publication year of the patents, but these effects are mainly important for the most recent year. All searches for the period 2000-2006 were therefore repeated on December 13, 2007.
[8] Numbers for Tokyo University are based on adding “Tokyo University” and “University of Tokyo” as search terms.